About Vieta's Formula
The coefficients of polynomials are related to the sums and products of their roots, as well as the products of the roots obtained in groups, using Vieta's formulas, also known as Viète's laws. Francois Viete was the one who discovered it. Vieta's formula in quadratics is the simplest application of Viete's formula and is used primarily in algebra. In the following section, we'll look at Vieta's formula in further depth.
Vieta's formulae are a collection of equations that relate polynomial roots and coefficients. Vieta's formulas for various situations are as follows:
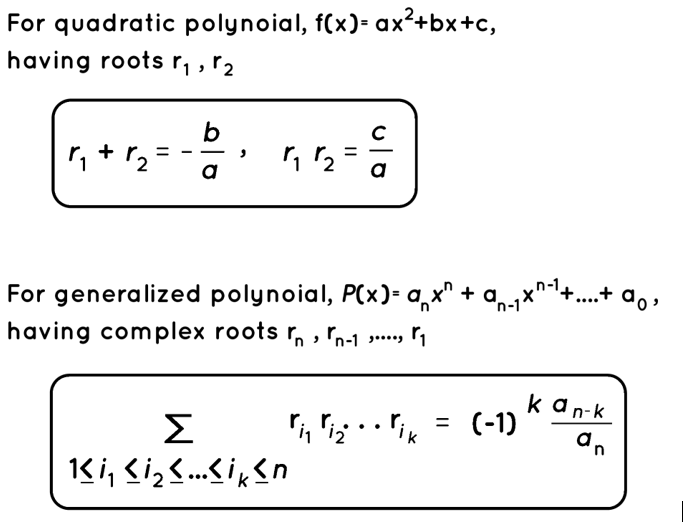
The Quadratic Formula of Vieta: If f(x) = ax2 + bx + c has roots f(x) = r1,r2, then the equation f(x) = 0 has roots f(x) = r1,r2.
r1+r2=−b/a , r1r2 = c/a
Vieta's Formula for Generalized Higher Degree Polynomials:
Let P(x)=anxn+an-1xn-1+.......+a0
be a polynomial of degree n with complex coefficients and complex roots
rn,rn-1,… r1. Then for any integer 0 ≤ k ≤n,
Download free pdf of Vieta's Formula Formula Its Use And Solved Examples
