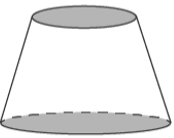
Frustum of Cone

The frustum of a cone is a portion of the cone that remains after it has been cut by a plane parallel to its base. Cones and pyramids have a frustum, which is also known as a truncated shape. Different forms of frustums exist, depending on the shape from which they are formed.

Frustum of cone
Frustum of a triangular pyramid
Frustum of a square pyramid, etc.

When a cone is divided into two sections by a plane parallel to the base of the cone, the frustum is the part of the cone without a vertex. A truncated cone is another name for the frustum of a cone. The frustum of a cone has surface area and volume, just like any other 3D object. In the following sections, we'll look at the formulas for locating them.

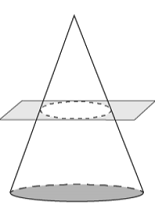A plane parallel to the base of the cone cuts it	→	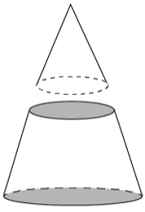Two parts are formed	→	The part with the base is the frustum of the cone

Net of Frustum of Cone
The frustum is the region of a cone without a vertex that is divided into two sections by a plane parallel to the base of the cone. The frustum of a cone is sometimes known as a truncated cone. A cone's frustum, like any other 3D object, has surface area and volume. We'll look at the formulas for locating them in the sections below. A frustum of cone can be formed as shown in the diagram below.

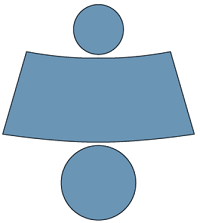Volume of Frustum of Cone
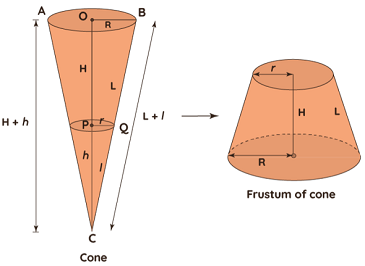
The volume of a cone's frustum is the amount of space it contains. The volume of frustum of a cone, like the volume of any other form, is measured in cubic units such as m³, cm³, in³, and so on. Consider a cone with a radius R at the base and a height H + h. Assume that frustum of cone of height H is created from the cone, with a high base radius 'R' and a tiny base radius 'r'. Let L and L + l be the frustum and cone slant heights, respectively. Volume of frustum of the cone can then be calculated using one of the formulas below.

Volume of frustum of the cone = πh/3 [ (R³- r³) / r ] (OR)
Volume of frustum of the cone = πH/3 (R²+ Rr + r²)

V = πh/3 [ (R³- r³) / 3 ] OR
V = πh/3(R²+ Rr³ + r²)

Note: π = 22/7 (or) 3.141592653...

Surface Area of Frustum of Cone
The area of the frustum of a cone is calculated by adding the areas of its faces. It is measured in square units such as m², cm², in², and so on because it is an area. Consider a cone with a slant height of L + l, a height of H + h, and a radius of R at its base. Assume the cone forms a frustum with height H, small base radius 'r,' large base radius 'R,' and slant height L. Here are the formulas for calculating the curved surface area (CSA) and total surface area (TSA) of a cone frustum. The frustum of the cone's curved surface area.

(CSA) is CSA (or) LSA of frustum of cone = πl [ (R²- r²) / r ] (OR) πL (R + r)
TSA of frustum of cone = πl [ (R²- r²) / r ] + π (R²+ r²) (OR) πL (R + r) + π (R²+ r²)