Worksheet for class 7 Maths 

Class 7 Maths Worksheets

Worksheets for class 7 Maths are created by CBSE teachers of HT and consist of MCQ-based questions chapter-wise as per the CBSE syllabus. All the chapters of class 7 Maths are uploaded in printable worksheets and easily downloaded forms. Maths is a subject of practice and understanding the concept to have a good foundation of conceptual clarity on maths do read the chapter from NCERT and solve all the questions asked in the exercise you can take help from HT NCERT solutions for class 7 Maths. After this one can solve the questions from Worksheet for class 7 Maths. 

 

Find the questions from Worksheet for class 7 Maths 

Questions Answer Set-1 

Q1. Vidya’s mother’s age is 5 years more than three times of Vidya’s present age. Find Vidya’s present age, if his mother is 44 years old.

(a) 10 years (b) 16 years

(c) 13 years (d) 18 years

Ans.1. (c) Suppose Vidya’s age is the year

Then 3 y + 5 = 44

⇒ 3 y = 44 – 5 = 39

⇒ y = 13 years

Q2. The sum of four times a number and 12 is 36. Find the number?

(a) 7 (b) 4

(c) 6 (d) 5

Ans.2. (c) If the unknown number is taken to be x,

then four times the number is 4 x and

the sum of 4x and 12 is 36

that is, 4 x + 12 = 36

To solve this equation, we transpose 12 to R.H.S,

So that 4x = 36 –12 = 24

⇒ x = 6

Q3. A shopkeeper sells apples in two types of boxes, one small and one large. A large box contains double as many as small boxes plus 6 loose mangoes. The number of mangoes in a large box is given to be 100. Then the number of apples in small box is

(a) 47 (b) 48

(c) 49 (d) 35

Ans.3. (a) Let small box contain ‘m’ mangoes

Then according to the given equation 2m + 6 = 100

⇒ m = 100-6/2 = 94/2 = 47

Q4. Which of the following is correct? Choose the answer from the code given below

I. The sum of numbers x and 4 is 9

In equation form, it is represented as x + 4 = 9

II. Seven times M plus 7 you 77

In equation form, it is represented as 7 M + 7 = 77

III. If you add 3 to one third of Z, you get 30.

In equation form, it is represented as 3+ Z/3 = 30

Code:

(a) I and II (b) II and III

(c) All are correct (d) All are incorrect

Ans.4. (c) All are correct.

I. x + 4 = 9

II. Seven times M is 7 M.

Sum of 7 M and 7 is 7M + 7

The sum is 77.

Hence the equation is 7 M + 7 = 77

III. One third of Z is Z/3

Sum of Z/3  and 3 is Z/3 + 3 .

The sum is 30.

Hence the equation is Z/3 + 3 =30

Q5. What are the values of p and m if 3p –1 = 23 and 6m – 2 = 34

(a) p = 6, m = 7 (b) p = 8, m = 6

(c) p = 6, m = 6 (d) p = 4, m = –6

Ans.5. (b) 3p –1 = 23 ⇒ 3p = 23 + 1 ⇒ p=8

and 6 m –2 = 34 ⇒ 6m = 36 ⇒ m = 6

Q6. Which of the following is correct?

I. 7m + 19/2=13 then m =1/2

II. 5t + 28 = 3, then t = –5

III. 5x –2 = 8, then x = 3

Code :

(a) I, III  (b) II & III

(c) I & II (d) All are correct

Ans.6. (c) I.7m= 13 - 19/2 = 26-19/2 = 7/2 

m=1/2

II. 5t = 3–28 = –25 ⇒ t = – 5

III. 5x –2 = 8 ⇒ 5x = 10, x = 2

Hence, I and II are correct.

Q7. Sachin says that he has 6 books more than the 6 times of the books Priyanka has. Sachin has 42 books. How many books does Priyanka have?

(a) 8 (b) 6

(c) 9 (d) 10

Ans.7. (b) Let Priyanka has p books.

Then according to the question 6p + 6 = 42 ⇒ p = 6

Q8. The teachers tell the class that the lowest marks obtained by a student in her class are one-forth the highest marks plus 8 is 33. What is the highest score?

(a) 90 (b) 100

(c) 60 (d) 200

Ans.8. (b) Let H be the highest marks.

Then according to the question, H/4 + 8 = 33 ⇒ H = (33 – 8) 4 = 100

Q9. In an isosceles triangle, the base angles are equal and the vertex angle is 50°. What are the values of base angles of the triangles?

(a) 60 ° (b) 45°

(c) 65° (d) None of these

Ans.9. (c) Let each of the base angle is θ.

Then equation is 2θ + 15 = 180

⇒ θ = 180-50/2 = 130/2 = 65°

Q10. Laxmi takes away 7 from 5/2  of the number, the result is 11/2  . Then the number is

(a) 11/2 (b) 5/2

(c) 11 (d) 5

Ans.10. (d) Let numbers is x

then equation is 5/2 x -7=11/2

⇒ 5x/2=11/2 +7=25/2

⇒ x = 5

Q11. The solution of 3(b + 2)–(b – 8) = 3(b + 8) is

(a) –10 (b) 10

(c) 2 (d) –3

Ans.11. (a) 3 (b + 2) – (b –8) = 3(b +8)

3b + 6 – b + 8 = 3b + 24

2b + 14 = 3b + 24

b = –10

Q12. A student has to secure 35% marks to pass. He got 80 marks and failed by 60 marks. Find the maximum marks.

(a) 100 (b) 200

(c) 300 (d) 400

Ans.12. (d) 35/100 x = 80 + 60

35/100 x= 140  ⇒ x = 400

Q13. There were only two candidates who participated in an election. One contestant got 62% votes and was elected by a margin of 144 votes. The total number of votes were

(a) 500 (b) 600

(c) 700 (d) 800

Ans.13. (b) Elected candidate got  62x/100 votes. Other candidates got 38x / 100 votes. We have,

⇒62x/100-38x/100=144

24x/100=144⇒ x = 600

Q14. In a coconut grove, (x + 2) trees yield 60 nuts per year, x trees yield 120 nuts per year and (x –2) trees yield 180 nuts per year. If the average yield per year of all trees be 100, then find x.

(a) 4 (b) 3

(c) 2 (d) 1

Ans.14. (a)

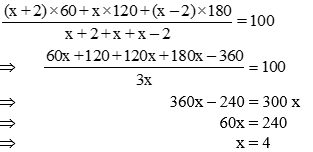
Q15. The average of 11, 12, 13, 14 and x is 13. The value of x is

(a) 17 (b) 21

(c) 15 (d) None of these

Ans.15. (c)

11+12+13+14+x/5 =13

x = 65 – 50

x = 15

Q16. The average of three numbers is 60. The first is 1/4 th of the sum of the other two . The first number is

(a) 24 (b) 36

(c) 48 (d) 72

Ans.16. (b) Let a, b and c are three numbers.

a+b+c /3 =60

a + b +c = 180

and a=1/4(b+c) = 1/4(180-a)

4a = 180 –a

a= 180/5 =36

Q17. The ratio between two numbers is 3 : 5. If each number is increased by 4, the ratio becomes 2:3. Find the numbers.

(a) 12,20 (b) 18,30

(c) 24,40 (d) 15,25

Ans.17. (a) Let the numbers be 3x, 5x

3x+4/ 5x+4 =2/3 

9x + 12 = 10x + 8

x = 4

⇒The numbers are 3 × 4, 5 × 4 = 12, 20

Q18. 4 is added to a number and the sum is multiplied by 5. If 20 is subtracted from the product and the difference is divided by 8, the result is equal to 10. Find the number.

(a) 16 (b) 12

(c) 8 (d) 20

Ans.18. (a) Let the number be x.

(x+4) × 5-20/8 =10

5x + 20 – 20 = 80

x = 16

Q19. One number is 3 less than the two times of the other. If their sum is increased by 7, the result is 37. Find the numbers.

(a) 9,11 (b) 11,13

(c) 11,19 (d) 9, 13

Ans.19. (c) Let one number = x

Other number = 2x – 3

(x + 2x –3)+ 7 = 37

3x = 33

x = 11

Q20. 1/2 is subtracted from a number and the difference is multiplied by 4, then 25 is added to the product that sum is divided by 3, the result is equal to 10. Find the number.

(a) 3/5 (b) 7/4

(c) 6/7 (d) None of these

Ans.20. (b) Let the number be x.

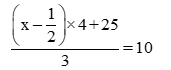
⇒ 4x – 2 + 25 = 30

⇒ 4x = 7

⇒ x= 7/4 

Q21. The present age of A is twice that of B. 30 years from now, age of A will be 1½  times that of B. Find the present ages of A and B respectively.

(a) 60, 30 (b) 30, 60

(c) 40, 50 (d) 50, 40

Ans.21. (a) Present age: A = 2x, B = x

After 30 years: A = 2x + 30, B = x + 30

So 2x + 30 = 1½ (x + 30)

⇒ 4x + 60 = 3x + 90

⇒ x = 30

Q22. The present age of a man is 3 times that of his son. Six years ago, the age of the man was four times that of his son. Find the ratio of their ages six years later.

(a) 4 : 3 (b) 3 : 4

(c) 2 : 5 (d) 5 : 2

Ans.22. (d) Let present age of son = x years

Present age of man = 3x

Six years ago

Age of man = 3x –6

Age of son = x –6

3x –6= 4(x –6)

3x –6= 4x –24

x = 18

Six years after

Age of man = 3 × 18 + 6 = 60

Age of son = 18 + 6 = 24

Required Ratio = 60 : 24 = 5 : 2

Q23. The total cost of three prizes is Rs. 2550. If the value of the second prize is 3/4 th of the first and the value of 3rd prize is 1/2 of the second prize, find the value of the first prize.

(a) Rs 900 (b) Rs 1500

(c) Rs 1200 (d) Rs 450

Ans.23. (c) Let first prize = x

Second prize =3/4x

Third Prize = 1/2  3x/4= 3x/8

x+3x/4+3x/8=2550

17x/8 = 2550.

x = 1200

Q24. The sum of 4 consecutive integers is 70. Then the greatest among them is

(a) 19 (b) 23

(c) 17 (d) 16

Ans.24. (a) The consecutive integers are x, x +1, x+2, x+ 3.

x + x+ 1 + x + 2+ x+ 3 = 70

⇒ 4x + 6 = 70

⇒ 4x = 64

⇒ x = 16

⇒ Greatest number = x + 3 = 16 + 3 = 19.

Q25. If two supplementary angles are differ by 44° then one of the angle is

(a) 102° (b) 65°

(c) 112° (d) 72°

Ans.25. (c) The angles are x, x – 44°

So x + x – 44° = 180°

2x = 224°

x = 112°

07 - Mat

Questions Answer Set-2

Chapter – 04

TQ=25

Q1. If one third of x plus 9 is 12. Then the value of x is

(a) 1 (b) 9

(c) 3 (d) 12

Ans.1. (b) One third of x = x/3

According to question, x/3 +9 = 12

x/3 = 12 - 9 = 3

x/3 =  3/1, x = 3 3 = 9

x = 9

Q2. The sum of four times x and 6 is 34, its statement in the form of

equation is

(a) 4x - 6 = 34 (b) 4x - 34 = 6

(c) 4x + 6 = 34 (d) x/4 + 6 = 34

Ans.2. (c) Four times of x = 4x

Then, according to question

4x+6 = 34

Q3. What is the value of p, if (5p -2) = (1 +2p)

(a) 2 (b) 1

(c) 3 (d) 4

Ans.3. (b) (5p -2) = (1 +2p)

5p - 2p = 1 + 2

3p = 3, p = 3/3 = 1

Q4. The equation 3p +6 = 21 in the statement form is

(a) Two times of p and plus 6 is 21.

(b) Three times of p and plus 6 is 21.

(c) Four times of p and plus 6 is 21.

(d) Three times of x and plus 6 is 21.

Ans.4. (b) Three times of p = 3p

3p plus six is 21, 3p +6 = 21

Q5. What is the value of q, if 2q + 6 = 12

(a) 2 (b) 1

(c) 3 (d) -1

Ans.5. (c) The given equation is 2q + 6 = 12

subtracting 6 on both the sides

2q + 6 - 6 = 12 -6,

2q = 6 ( dividing by 2 on both the sides)

q = 3

Q6. What is the value of a, if a/3 = 7/4

Ans.6. (a)

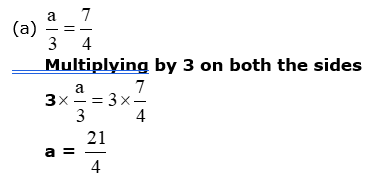
Q7. Solution of 2y + 5/2 = 37/2 is

(a) 6    (b) 8

(c) 10  (d) 12

Ans.7. (b) 2y + 5/2 = 37/2

2y = 37/2 - 5/2 (transposing 5/2 to R.H.S)

2y = 37-5 / 2 = 32/2 =16

2Y = 16

Y =16/2 = 8

Q8. -4(x - 2) = 16, the value of x is

(a) 2 (b) -1

(c) 1 (d) -2

Ans.8. (d) -4(x - 2) = 16

Dividing by (-4) on both the sides, we have

(x – 2) = -4

x = -4 +2 transposing (-2) to R.H.S

x = -2

Q9. The sum of three consecutive integers is 21. The least integer is ……..

(a) 9 (b) 6

(c) 18 (d) 21

Let three consecutive integers be x, x+1 and x+2.

Ans. 9.(b)

According to question

x + x+1 +x+2 = 21

3x + 3 = 21

3x = 21 -3 = 18

3x = 18, x = 18/3 = 6

Q10. Shanu’s father’s age is 6 years more than three times shanu’s age.

Find shanu’s age, if his father is 48 years old.

(a) 14 (b) 12

(c) 16 (d) 18

Ans.10. (a) Let shanu’s age be x.

According to question

Three times of shanu’s age + 6 = shanu’s father age’s

3x + 6 = 48

3x = 48 - 6 = 42

3x = 42, x = 14

Q11. The length of a reactangle is twice of its breadth. If the perimeter of

the reactangle is 18 cm, then the area of its reactangle is…….

(a) 72 sq cm (b) 36 sq cm

(c) 18 sq cm (d) 49 sq cm

Ans.11. (c) Let breadth of the given reactangle is x.

Then length of its reactangle = 2x

perimeter = 2(length + breadth)

2(2x + x) = 18

3x = 18/2 = 9

x = 9/3 = 3 cm

breadth = 3 cm

length = 2 3 = 6 cm

Area of the given reactangle = length breadth

area = 6 3 = 18 sq cm

Q12. What is the value of t? If 4 + 3(t + 2) = 10.

(a) 1 (b) 2

(c) 0 (d) -1

Ans.12. (c) 4 + 3(t + 2) = 10

3(t + 2) = 10 – 4 (transposing 4 to R.H.S)

3(t + 2) = 6

dividing by 3 on both the sides

(t + 2) = 2

t = 2 - 2 = 0

t = 0

Q13. What is the number one third of which added to 5 gives 6?

(a) 4 (b) 3

(c) 1 (d) 2

Ans.13. (b) Let the number be x.

According to question

x/3 + 5= 6 

x/3 = 6 – 5

x/3 = 1, x = 3 × 1 = 3

The required number is 3.

Q14. Sachin scored twice as many runs as rahul. Together, their runs fell two short of a double century. How many runs did each one score?

(a) 122 and 61 (b) 132 and 66

(c) 112 and 56 (d) 66 and 132

Ans.14. (b) Let rahul’s score be x.

Then sachin’s score will be 2x.

According to question

x + 2x = 198

3x = 198

x = 198/3 = 66

and 2x = 2 66 = 132

Hence sachin and rahul score’s are 132 and 66 respectively.

Q15. Isha subtracts thrice the number of notebooks she has from 44, he find the result 5. What is the number?

(a) 14 (b) 13

(c) 12 (d) 15

Ans.15. (b) Let the required number be x.

According to question

44 – 3x = 5

- 3x = 5 – 44 (transposing 44 to R.H.S)

- 3x = -39

dividing by (-3) on both the sides

x = 13

Q16. Average of 1, 3, 5, x, 8 is 9. The value of x will be

(a) 18 (b) 27

(c) 8 (d) 28

Ans.16. (d) Average = (sum of observation)/ number of observation

9 = 1+3+5+x+8 / 5

x+17/5 = 9/1

x + 17 = 45

x = 45 – 17 = 28

Q17. If two complementary angles are differ by , then one of the angle

is ……

(a) 58° (b) 36°

(c) 46° (d) 30°

Ans.17. (a) Iet the angles are x, (x - 26 ° )

x + x - 26° = 90°

2x = 90° + 26° =  116°

x = 116°/2 = 58°

Q18. In an isosceles triangle, the base angles are equal. The vertex angle is . What are the base angles of the triangle?

(a) 75° (b) 65°

(c) 45° (d) 55°

Ans.18. (a) Let the base angle of given triangle is x.

We know that sum of all angles of a triangle is 180°.

x + x + 30° = 180°

2x =180° - 30° = 150°

x = 150° /2 = 75°

Q19. Two-fifth of a number minus 5 gives 3. The number is

(a) 10 (b) 30

(c) 20 (d) 40

Ans.19. (c) Let required number be x.

According to question,

2x/5-5 =3

2x/5=3+5= 8

2x/5= 8/1

x =8 × 5 /2 = 4 × 5 = 20

Q20. Uttam thinks of a number. If he takes away 5 from 7/2 of the number,

the result is 11/2 . The number will be

(a) 4 (b) 3

(c) 5 (d) 6

Ans.20. (b) Let the required number be x.

According to question,

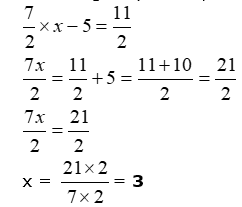
Q21. Amit‘s father is 69 years old. He is 4 years older than five times Amit’s

age. What is Amit’s age?

(a) 12 (b) 17

(c) 14 (d) 13

Ans.21. (d) Let amit’s age be x.

Then according to question

five times amit’s age + 4 = amit’s father age

5x + 4 = 69

5x = 69 – 4 = 65, x = 65/5 = 13

Q22. When I subtract 7 from twice a number, the result was 9. What is the

number?

(a) 6 (b) 8

(c) 9 (d) 7

Ans.22. (b) Let the number be x.

According to question,

2x – 7 = 9

2x = 9 + 7 =16

x = 16/2 = 8

Q23. If two supplementary angles are differ by then one of the angle is

(a) 116°  (b) 117°

(c) 118°  (d) 54°

Ans.23. (b) Let the angles are x and (x - 54° ).

Then, x + x - 54° =118°

2x = 180° + 54° = 234°

x = 234° /2 =117°

Q24. If (3x - 7/2 ) = (x + 3/2). Then the value of x is ……

(a) 3/2  (b) 5/2

(c) 7/2  (d) 9/2

Ans.24. (b) (3x - 7/2  ) = (x + 3/2 )

3x – x = 3/2 + 7/2 = 3+7/2

2x = 10/2 = 5

x = 5/2

Q25. If ( 7x/3 - 4/3= x/2 +3/2 ), then the value of x is …….

(a) 16/11 (b) 15/11

(c) 17/10 (d) 17/11

Ans.25. (d)

 

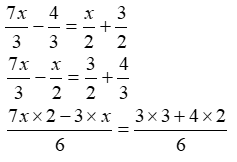
Chapter - 3

Data Handling

[1 Mark for Each Question]

Q 1: The mean of first five multiples of 4 is

(a) 10.

(b) 11.

(c) 12.

(d) 14.

Ans: (c)

Explanation:

We know that first five multiples of 4 are 4, 8, 12, 16, and 20.

Thus Mean = 4+8+12+16+20 / 5 = 60/5 = 12

Q 2: The mean of first four prime number is

(a) 2.5.

(b) 4.25.

(c) 5.

(d) 17.

Ans: (b)

Explanation:

First four prime numbers are 2, 3, 5 and 7.

 Mean = 2+3+5+7 / 4 = 17/4 = 4.25

Q 3: The median of the given set of numbers 23, 42, 20, 16, 30 is

(a) 20.

(b) 16.

(c) 23.

(d) 42.

Ans: (c)

Explanation:

First we arranging the given numbers in ascending order, we get

16, 20, 23, 30, 42.

Since, median is the middle observation in the given data.

Therefore, median = 23.

Q 4: The scores in mathematics test of 8 students are 19, 25, 23, 20, 9, 20, 15 and 10. The median of the test scores of this data will be

(a) 19.5.

(b) 19.7.

(c) 19.8.

(d) 20.

Ans: (a)

Explanation:

Arranging the given numbers in ascending order, we get

9, 10, 15, 19, 20, 20, 23, 25

Here the number of observations is 8, i.e., an even number.

Hence the median of the data

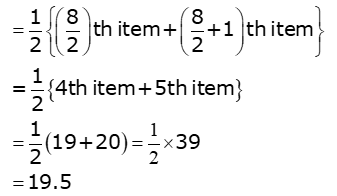
Therefore, median = 19.5.

Q 5: The mode of the given set of numbers 1, 3, 2, 5, 1, 4, 6, 2, 5, 2, 2, 4, 1, 2 is

(a) 1.

(b) 2.

(c) 4.

(d) 5.

Ans: (b)

Explanation:

Arrange the given data in ascending order with same value together, we have

1, 1, 1, 2, 2, 2, 2, 2, 3, 4, 4, 5, 5, 6

Here maximum frequency of 2 = 5

Therefore, mode = 2.

Q 6: The mode of the given set of numbers 2, 6, 5, 3, 0, 3, 4, 3, 2, 4, 5 is

(a) 2.

(b) 3.

(c) 2 and 4.

(d) 2 and 3.

Ans: (b)

Explanation:

Arranging the given data in ascending order, we get

0, 2, 2, 3, 3, 3, 3, 4, 4, 5, 6. Here 3 is occurring maximum number of times.

Therefore, mode = 3

Q 7: The mean of all prime numbers between 25 and 45 is

(a) 10.

(b) 35.

(c) 36.2.

(d) 40.

Ans: (c)

Explanation:

Prime Numbers between 25 & 45  are 29,31,37,41,43

Mean = 29+31+37+41+43 / 5 = 181/5 = 36.2

Q 8: The mean of the first five multiple of 7 is

(a) 20.

(b) 21.

(c) 22.

(d) 23.

Ans: (b)

Explanation:

 

The first five multiple of 7 are 7.14,21,28 & 35

Mean = 7+14+21+28+35 / 5 = 105/5 = 21

Q 9: The mean of the first six whole numbers is

(a) 2.

(b) 2.2.

(c) 2.5.

(d) 3.

Ans: (c)

Explanation:

 First Six whole numbers are 0,1,2,3,4 & 5

 Mean = 0+1+2+3+4+5 / 6 = 15/5 = 2.5

Q 10: If the mean of 7, 14, p, 9 and 16 is 11.5, then the value of p will be

(a) 7.

(b) 9.

(c) 10.

(d) 11.5.

Ans: (d)

Explanation:

Q 11: The mean of 6 numbers is 12. If 3 is subtracted from every number, then the new mean will be

(a) 9.

(b) 10.

(c) 11.

(d) 12.

Ans: (a)

Explanation:

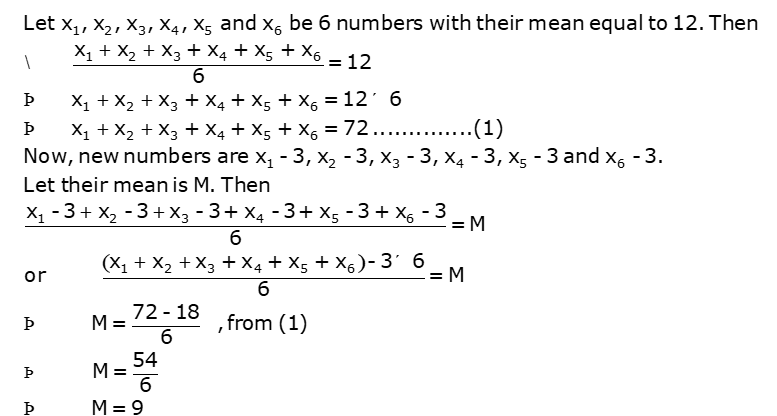
Q 12: If the mean of five observations a, a+2, a+4, a+6 and a+8 is 11, then the mean of first three observations will be

(a) 7.

(b) 9.

(c) 10.

(d) 15.

Ans: (b)

Explanation:

Q 13: Range of the given set of a data 11, 13, 17, 19, 23, 25, 29 is

(a) 11.

(b) 17.

(c) 18.

(d) 19.

Ans:(c)

Explanation:

Since,

The highest value in the given data = 29

And, the lowest value in the given data = 11

We know that, range = highest value - lowest value

Therefore, range = 29 - 11 = 18

Q 14: Range of the given set of a data 22, 24, 26, 28, 30, 32, 34, 36 is

(a) 14.

(b) 22.

(c) 28.

(d) 36.

Ans:(a)

Explanation:

Since,

The highest value in the data = 36

And the lowest value = 22

And we know that

Range = highest value - lowest value

Therefore, range = 36 - 22 = 14

Q 15: For comparing two collections of data at a glance we use

(a) pie graph.

(b) bar graph.

(c) double bar graph.

(d) column graph.

Ans:(c)

Explanation:

Double bar graph helps to compare two collections of data at a glance.

Q 16: The range of a given data is

(a) lowest value – highest value.

(b) highest value/ lowest value.

(c) highest value + lowest value.

(d) highest value – lowest value.

Ans:(d)

Explanation:

Range is the difference between the highest and the lowest value in a data set.

Q 17: The 9 tall trees in a park have heights (in metre) 42, 35, 45, 39, 47, 52, 58, 61 and 64. The median of their heights is

(a) 42.

(b) 45.

(c) 47.

(d) 64.

Ans:(c)

Explanation:

First we arrange the given heights of 9 trees in ascending order, we have

35, 39, 42, 45, 47, 52, 58, 61, 64.

Since, median is the middle observation in the given data.

And here median is 5th observation, i.e., 47.

Q 18: In a given data set, median gives the

(a) first value.

(b) middle value.

(c) last value.

(d) first and last values.

Ans:(b)

Explanation:

Median gives the middle observation in a given data set.

Q 19: The heights of 10 girls were measured in cm are 130, 128, 145, 129, 138, 147, 144, 152, 150 and 146. The range of the data is

(a) 24.

(b) 128.

(c) 152.

(d) 280.

Ans:(a)

Explanation:

On arranging the given data in ascending order, we get

128, 129, 130, 138, 144, 145, 146, 147, 150, 152.

Since, range = highest value – lowest value.

Thus, range = 152 - 128 = 24

Q 20: In rolling a dice, the possible outcomes are

(a) one.

(b) two.

(c) six.

(d) ten.

Ans:(c)

Explanation:

In rolling a dice, there are six possible outcomes i.e. 1, 2, 3, 4, 5 and 6.

Q 21: The probability of getting 4 on a dice will be

(a) 1/2

(b) 1/4

(c) 1/5

(d) 1/6

Ans:(d)

Explanation:

Since, Probabiltiy = Favourable Trials / Total No of Trials

Hence Probabilty of getting 4 on a dice = 1/6

Q 22: The probability of getting a spade from a well-shuffled pack of cards will be

(a) 1/4

(b) 1/13

(c) 1/52

(d) 4.

Ans:(a)

Explanation:

There are 13 spades out of 52 cards in a well-shuffled pack of cards.

Therefore the probability of getting a spade is 13/52 = 1/4

Q 23: The probability of getting a face card from a well-shuffled pack of cards will be

(a) 1/4

(b) 1/13

(c) 1/52

(d) 3/13

Ans:(d)

Explanation:

There are 12 face cards out of 52 cards in a well-shuffled pack of cards.

Therefore the probability of getting a face card will be 12/52 = 3/13

Q 24: The probability of getting a queen from a well-shuffled pack of cards will be

(a) 1/4

(b) 1/13

(c) 1/52

(d) 4.

Ans:(b)

Explanation:

Since, there are 4 queens out of 52 cards in a well-shuffled pack of cards.

Therefore the probability of getting a queen will be 4/52 = 1/13

Q 25: There are 6 balls in a bag with numbers from 1 to 6 marked on each of them. The probability of drawing a ball with number 3 will be

(a) 1/2

(b) 1/3

(c) 1/5

(d) 1/6

Ans:(d)

Explanation:

Since, Probabiltiy = Favourable Trials / Total No of Trials

Hence Probabilty of getting a ball with number 3 = 1/6