About Perfect Square Trinomial Formula
Perfect square trinomials are three-term algebraic expressions generated by multiplying a binomial with another binomial. A perfect square is the result of multiplying two numbers by themselves. Binomial expressions are algebraic expressions with only two terms separated by a positive (+) or negative (-) sign. Trinomials, on the other hand, are algebraic expressions with three terms. When you multiply a binomial with a variable and a constant by itself, you get a perfect square trinomial with three terms. A positive or a negative sign separates the terms of a perfect square trinomial.
Perfect Square Trinomial Definition
An algebraic expression formed by squaring a binomial expression is known as a perfect square trinomial. It has the following formula: ax2 + bx + c. Here, a, b, and c are all real numbers, and a is not equal to zero. Consider the case of a binomial (x+5) multiplied by (x+4). The final result is x2 + 9x + 20. A perfect square trinomial can be decomposed into 2 binomials, which can then be multiplied together to form a perfect square trinomial.
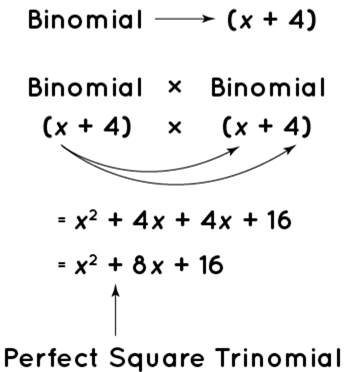
Perfect Square Trinomial Pattern
Perfect square trinomial has a pattern of a2 + 2ab + b2 or a2 - 2ab + b2.
To find the perfect square trinomial follow these steps:-

The square of the first term of the binomial is the first term of the perfect square trinomial. The second term is twice the product of the binomial's two components, and the third term is the square of the binomial's second term. To comprehend the perfect square trinomial pattern, look at the diagram below. If the binomial being squared has a positive sign, all of the terms in the perfect square trinomial are positive; but, if the binomial's second term has a negative sign, the trinomial's second term (which is twice the product of the two variables) will be negative.

How to Factor Perfect Square Trinomial?
- Between the terms of perfect square trinomials, a positive or negative symbol is used to separate them. The following are two key algebraic identities related to perfect square trinomials.
- (a + b)2 = a2 + 2ab + b2
- (a - b)2 = a2 - 2ab + b2
To factor a perfect square polynomial follow these steps :

Perfect Square Trinomial Formula
Multiplying the same binomial equation with each other yields a perfect square trinomial. If a trinomial has the form ax2+bx+c and also meets the requirement, it is said to be a perfect square b2 = 4ac. There are 2 forms of a perfect square trinomial. They are,
- (ax)2+ 2abx + b2= (ax + b)2----- (1)
- (ax)2−2abx + b2 = (ax−b)2----- (2)
Get a List of Maths Formulas on one page