Trigonometry Formulas

About Trigonometry Formulas

Trigonometry formulas are a set of the different formulas involving Trigo identities, applied to evaluate problems based on the sides and angles of a right-angled triangle. These trigo formulas include Trigo functions like sin, cos, tan, cosec, sec, cot for the given angles. Get the List of all Maths formulas in one place.

List of Trigo Formulas

Trigonometric formulas can be divided into different categories based on Trigo identities involved. Now take a look at the below sets of different trigo formulas.

Basic Trigo Ratio Formulas: There are few trigo formulas relating to the basic trigo ratios sin, cos, tan, etc.

Reciprocal Identities: This involves trigo formulas dealing with reciprocal relation between trigo ratios.

Trigo Ratio Table: Trigo values are given for standard angles in trigo table.

Periodic Identities: These comprise trigo formulas which help in finding values of trigo functions for a shift in angles by π/2, π, 2π, etc.

Co-function Identities: Trigo formulas for co-function identities depict inter-relationships between trigo functions.

Sum and Difference Identities: These trigo formulas are evaluated to find value of trigo function for sum or difference in angles.

Half, Double and Triple Identities: These trigo formulas involve values of trigo functions for multiple angles.

Sum to Product Identities: These trigo formulas are evaluated to represent product of trigo functions as their sum or vice-versa.

Inverse Trigo Formulas: Inverse trigo formulas include formulas related to inverse trigo functions like sin inverse, cos inverse, etc.

Sine law and Cosine law

Some basic trigo formulas can be observed in image below.

In Right Triangle ABC

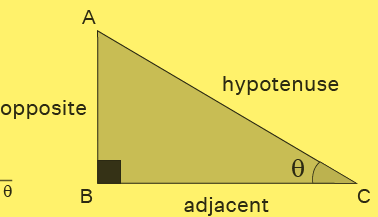Trigonometric formulas

Trigonometric formulas

Trigonometric formulas

Trigonometric formulas

Trigonometric formulas

Trigonometric formulas

 Trigonometric formulas

Basic Trigo Formulas

Basic trigo formulas are applied to evaluate the relation of trigo ratios and ratio of corresponding sides of right-angled triangle. There are 6 trigo ratios applied in trigo, written as sin, cos, sec, csc, tan, cot in short. The trigo functions and identities are derived using right-angled triangle as reference. We can find out sine, cosine, tangent, secant, cosecant, and cotangent values using trigo formulas as,

Trigonometric formulas

Trigo Ratio Formulas

  1. sinθ = Perpendicular / Hypotenuse
  2. cosθ = Base / Hypotenuse
  3. tanθ = Perpendicular / Base
  4. secθ = Hypotenuse / Base
  5. cosecθ = Hypotenuse / Perpendicular
  6. cotθ = Base / Perpendicular

Trigo Formulas involving Reciprocal Identities

Cose, sec, and cot are reciprocals of basic trigo ratios sin, cos, and tan. All of reciprocal identities are also derived using right angled triangle as reference. These reciprocal trigo identities are derived using trigo functions. The trigo formulas on reciprocal identities are used frequently to simplify trigo problems.

  1. cosecθ = 1 / sinθ
  2. secθ = 1 / cosθ
  3. cotθ = 1 / tanθ
  4. sinθ = 1 / cosecθ
  5. cosθ = 1 / secθ
  6. tanθ = 1 / cotθ

Trigo Ratio Table

Here is a table for trigo formulas for angles that are applied for solving trigo problems. The trigo ratios table helps in evaluating values of trigo standard angles as 0°, 30°, 45°, 60°, and 90°.

Angles(In Degrees) 0° 30° 45° 60° 90° 180° 270° 360°
Angles(In Radians) 0° π/6 π/4 π/3 π/2 π 3π/2 2π
sin 0 1/2 1/√2 √3/2 1 0 -1 0
cos 1 √3/2 1/√2 1/2 0 -1 0 1
tan 0 1/√3 1 √3 ∞ 0 ∞ 0
cot ∞ √3 1 1/√3 0 ∞ 0 ∞
cosec ∞ 2 √2 2/√3 1 ∞ -1 ∞
sec 2/√3 √2 2 ∞ -1 ∞ 1 ∞

Trigo formulas including periodic identities are applied to shift angles by π/2, π, 2π, etc. All trigo identities are cyclic that means they repeat their values after period. This period differs for different trigo formulas on periodic identities. As perr example, tan 30° = tan 210° but it’s not equal for cos 30° and cos 210°. We can use this to the trigo formulas given below to verify the periodicity of sin and cos functions.

  1. First Quadrant:
    1. sin(π/2 - θ) = cosθ
    2. cos(π/2 - θ) = sinθ
    3. sin(π/2 + θ) = cosθ
    4. cos(π/2 + θ) = - sinθ
  2. Second Quadrant
    1. sin(3π/2 - θ) = -cosθ
    2. cos(3π/2 - θ) = -sinθ
    3. sin(3π/2 + θ) = -cosθ
    4. sin(3π/2 + θ) = sinθ
  3. Third Quadrant
    1. sin(π - θ) = sinθ
    2. cos(π - θ) = -cosθ
    3. sin(π + θ) = -sinθ
    4. sin(π + θ) = -cosθ
  4. Fourth Quadrant
    1. sin(2π - θ) = -sinθ
    2. cos(2π - θ) = cosθ
    3. sin(2π + θ) = sinθ
    4. cos(2π + θ) = cosθ

Trigonometry Formulas Involving Co-function Identities(in Degrees)

The trigonometry formulas on cofunction identities provide the interrelationship between the different trigonometry function

  1. sin(90° - x) = cos x
  2. cos(90° - x) = sin x
  3. tan(90° - x) = cot x
  4. cot(90° - x) = tan x
  5. sec(90° - x) = cosec x
  6. cosec(90° - x) = sec x

Trigonometry Formulas Involving Sum and Difference Identities

The sum and difference identities include the trigonometry formula of sin(x + y),cos(x - y),cot(x + y),etc

sin(x + y) = sin(x)cos(y) + cos(x)sin(y)

cos(x + y) = cos(x)cos(y) - sin(x)sin(y)

Trigo Formulas Including Sine and Cosine Laws

Sine Law: Sine law and Cosine law give a relation between sides and angles of triangle.Sine law gives ratio of sides and angle opposite to side.As per example,ratio is taken for side 'a' and its opposite angle 'A'.

(sinA)/a = (sinB)/b = (sinC)/c

cosine Law:Cosine law helps to find length of aside,for given lengths of other two sides and included angle.As per example length 'a' can be found with help of other two sides 'b' and 'c' and their included angle'A'.

a2 = b2+ c2- 2bc cosA

b2 = a2+ c2- 2ac cosB

c2 = a2+ b2- 2ab cosc

Where,a,b,c are the lengths of the sides of the triangle, A,B,C are the angles of the triangle.

Download free pdf of Trigonometry Formulas Its Use And Solved Examples

Trigonometry Formulas
Trigonometry Formulas
Trigonometry Formulas
Trigonometry Formulas
Trigonometry Formulas

Related Links

Frequently Asked Questions on Trigonometry Formulas