About SAS Triangle Formula
Let's review what congruence and similarity are before understanding the SAS triangle formula. All related angle pairs and all corresponding sides are equal when triangles are congruent. All related angle pairs are equal and all corresponding sides are proportionate if two triangles are similar. However, we don't need to know about all sides and angles to be sure that the two triangles are identical or congruent. When two sides & the angle between these sides for both triangles meet the required condition, congruency or resemblance of any two triangles can be tested using the SAS Triangle Formula.
| Similar | Congruent |
|---|---|
 |
 |
To prove the congruence or resemblance of two triangles, various SAS Triangle formulas are utilised. SAS is an acronym for Side-Angle-Side.
SAS Congruence Rule
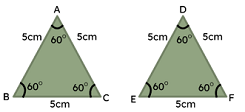
The Side-Angle-Side theorem of congruency asserts that two triangles are congruent if two sides and the angle created by these two sides are equivalent to two sides and the included angle of another triangle.
The SAS Similarity Rule
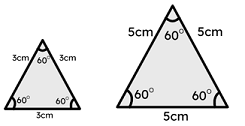
If two sides of one triangle are proportionate to two corresponding sides of another, and the included angles are equal, the two triangles are similar, according to the SAS similarity criterion.
| Similar and Congruent | Similar and not Congruent |
|---|---|
 |
 |
 |
 |
(SAS SIMILARITY)
Theorem: If one angle of a triangle is equal to one angle of the other and the sides including these angles are proportional than the two triangles are similar.
Given: 2 triangles ABC and DEF such that ∠A = ∠D and AB/DE = AC/DF
To prove: ABC ~ DEF
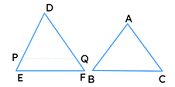
Construction: Let P & Q be points on DE & DF respectively such that DP = AB & DQ = AC. Join PQ.
Proof:
- In ABC and DPQ, we have
- AB = DP [By construction]
- AC = DQ [By construction]
- ∠A = ∠D [Given]
- ABC DPQ [By SAS congruency] ...(i)
- Now = AB/DE = AC/DF ...(ii)
- DP/DE = DQ/DF [ AB = DP and AC = DQ (by construction)]
- In DEF, we have
- DP/DE = DQ/DF [From (ii)]
- PQ || EF [By the converse of BPT]
- ∠DPQ = ∠DEF and ∠DQP = ∠DFE [Corresponding angles]
- DPQ ~ DEF [By AA similarity] …(iii)
- From equations (i) and (iii), we get
- ABC ~ DEF.
Download all the Maths formulas from the HT maths page.