A unit vector is one whose magnitude is equal to one. The "cap" symbol represents the unit vectors. Unit vectors have a length of one. Unit vectors are commonly used to indicate a vector's direction. A unit vector has the same direction as the given vector but a magnitude of one unit; for example, a unit vector for vector A is i, j, and k are unit vectors in directions of the x-axis, y-axis, and z-axis in a 3-dimensional plane. i.e. Get the List of all Maths formulas in one place. The numeric value of a vector is determined by its magnitude. A vector has both a magnitude and a direction. The magnitude of a vector formula is the sum of the vector's component measures along the x, y, and z axes. |A| is the magnitude of a vector A. The magnitude of a vector with the direction along the x-axis, y-axis, and z-axis can be calculated by taking the square root of the total of the square of its direction ratios. Let us begin by looking at the magnitude of a vector formula below. For a vector A = ai + bj + ck its magnitude is: |A| = Unit Vector is represented by ‘^’, which is called a cap, such as An arrow There are two ways to express a vector: The formula for determining a vector's magnitude is: |a| = The formula of the unit vector in the direction of a given vector is: Unit Vector = Vector/Vector's magnitude Simply divide a given vector by its magnitude to find a unit vector with the same direction. Take, for example, the vector v = (3, 4) with the magnitude |v|. We may derive the unit vector |v| = Thus, Vectors Properties The properties of vectors are helpful to gaining a detailed understanding of vectors and also in performing numerous calculations involving vectors, A few important properties of vectors are listed here.About Unit Vector
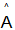 and
and 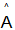 = (1/|A|)
= (1/|A|)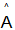
Vector’s Magnitude:
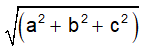
Unit Vector Notation
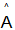 . It is given by
. It is given by 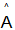 = a/|a| Where |a| is for norm or magnitude of vector a.
= a/|a| Where |a| is for norm or magnitude of vector a.Unit Vector Formula
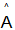 signifies a unit vector because vectors have both magnitude (Value) and direction (Direction). We divide every vector's magnitude by its unit vector to determine its unit vector. Any vector is usually represented by the coordinates x, y, and z.
signifies a unit vector because vectors have both magnitude (Value) and direction (Direction). We divide every vector's magnitude by its unit vector to determine its unit vector. Any vector is usually represented by the coordinates x, y, and z.
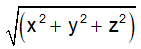
How to find the unit vector?
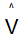 by dividing each component of vector v by |v|, which is in the same direction as v.
by dividing each component of vector v by |v|, which is in the same direction as v.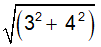 = 5
= 5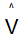 = v / |v| = (3, 4) / 5 = (3/5, 4/5).
= v / |v| = (3, 4) / 5 = (3/5, 4/5).
Download a free pdf of Unit Vector Formula Its Use And Solved Examples

