Square Root

About Square Root

Squaring a number is the inverse procedure of square rooting it. The square of a number is the result of multiplying it by itself, whereas the square root of a number is found by finding a number that when squared gives the original number. If 'a' is equal to the square root of 'b,' then a×a = b. Because the square of every integer is always a positive number, any number has two square roots, one positive and one negative. Both 2 and -2, for example, are square roots of 4. However, only the positive value of a number is expressed as the square root of a number in most places.

What do you mean by Square Root?

A number's square root is the element that, when multiplied by itself, returns the original number. Special exponents include squares and square roots. Take the number nine. When three is multiplied by itself, the result is nine. 3 × 3 or 32 are two ways to write this. We call this a square since the exponent is 2. When the exponent is 1/2, it now refers to the number's square root. √n = n1/2, for example, when n is a positive integer.

Definition of Square Root

The value of a number's square root is its power 1/2 value. To put it another way, it's the number whose product gives the original number. The symbol ‘√’ is used to represent it. The number under the square root sign is known as the radicand, whereas the square root symbol is known as a radical.

How to Find Square Root?

Finding the square root of a perfect square integer is fairly simple. Positive numbers that may be stated as the product of two numbers are known as perfect squares. Perfect squares, in other words, are integers that are represented as the power 2 of any integer. To find the square root of an integer, we can use one of the following four methods:

  1. Repeated Subtraction Method of Square Root
  2. Square Root by Prime Factorization Method
  3. Square Root by Estimation Method
  4. Square Root by Long Division Method

It's worth noting that the first three procedures are best for perfect squares, however the fourth approach, long division, can be used for any number, whether it's a perfect square or not.

Repeated Subtraction Method of Square Root

This is a really straightforward way. We remove consecutive odd numbers from the number we're looking for the square root of until we get to 0. The square root of the given integer is the amount of times we subtract. Only perfect square numbers operate with this strategy. Let's use this method to find the square root of 16.

  1. 16 - 1 = 15
  2. 15 - 3 =12
  3. 12 - 5 = 7
  4. 7- 7 = 0

You'll notice that we've deducted four times. Thus,√16 = 4

Square Root by Prime Factorization Method

Any number can be represented as a product of prime numbers using prime factorization. Follow the steps below to find the square root of a given number using the prime factorization method:

  1. Step 1: Find the prime factors of the given integer.
  2. Step 2: Create pairings of related factors in which both elements are equal.
  3. Step 3: Choose one of the two factors.
  4. Step 4: Take one factor from each pair and find the product of the factors.
  5. Step 5: The square root of the provided number is that product.
  6. Let's use this method to find the square root of 144.

Square Root of 144

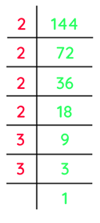
Square Root

144 = 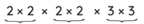Square Root

  1. =(2 x 2)x(2 x 2)x(3 x 3)
  2. =22 x 22 x 32
  3. =(2 x 2 x 3)2
  4. =(12)2
  5. 144 = (12)2
  6. √144 = 12

To get the list of Maths formulas check out the main page.

Find the pdf for downloading about Square Root

Square Root
Square Root

Related Links

Frequently Asked Questions on Square Root