About Tangent Line
One of the most prominent applications of differentiation is the "tangent line." Tangent is derived from the Latin word "tangere," which meaning "to touch." At one point on the curve, the tangent line hits it. To calculate the tangent line equation, we must first determine the curve's equation (which is given by a function) and the location where the tangent is drawn. The "point of tangency" is the location where the tangent is drawn. The tangent of a circle can be seen here.
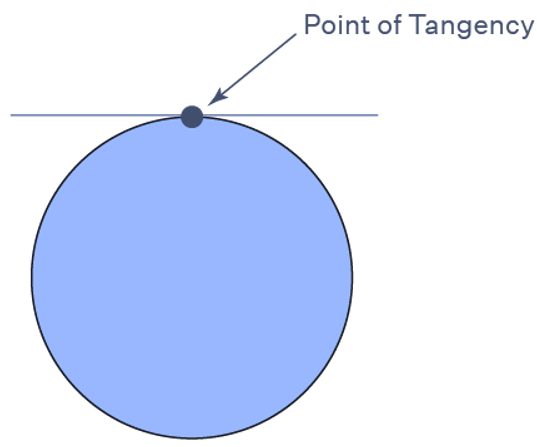
At a given point, the tangent line of a curve is a line that just touches the curve (function). In calculus, the tangent line may contact the curve at any other point(s) and cross the graph at any other point(s). It is not a tangent line of curve at each of the two points if a line travels through two points of the curve but does not contact the curve at either of the places. The line is known as a secant line in this circumstance. Check out the List of Maths Formulas.
Tangent Line Examples
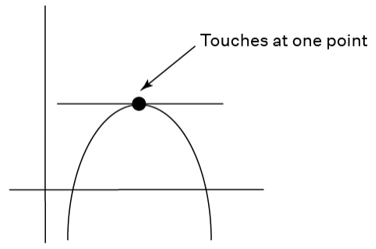
Here's an example of a tangent line that precisely touches the curve at one place.
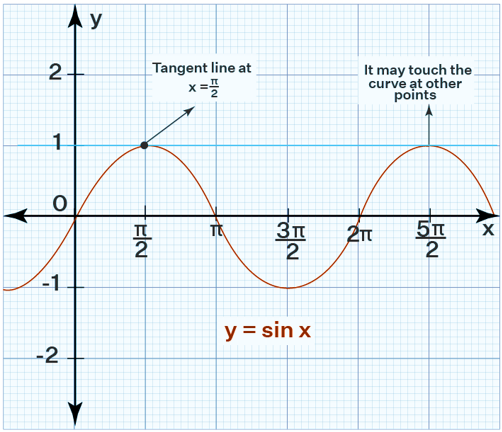
A tangent line can touch curve at multiple points.Here's an illustration.
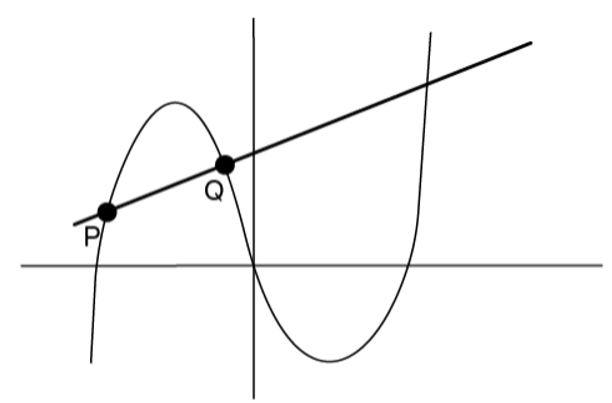
A curve's tangent line created at one point may also intersect the curve at another location. The tangent line, drawn at point P but crossing the curve at point Q, is shown here.
PQ might also be referred to as the secant line. A secant line can travel across any two points on the curve without having to touch it at each. The following diagram displays a secant line PQ that is not tangent at either P or Q.
Tangent Line Equation
tangent line formula is,
- y - y0 = (f '(x)) (?0, ?0) (x - x0)
Download free pdf of Tangent Line Its Use And Solved Examples
