About Parallelogram Formula
A two-dimensional shape is a parallelogram. It has four sides, two of which are parallel to each other. The lengths of the opposite sides of a parallelogram are identical, as are the measures of the opposite angles, and the sum of neighbouring angles is 180 degrees. Let's have a look at the properties of the parallelogram formula first.
Properties of a Parallelogram
- Opposite sides are parallel and congruent.
- Interior opposite angles are congruent.
- Consecutive angles are supplementary.
- In case, if the measure of any one of the angles is a right angle, then all the other angles will be the right angle.
- The 2 diagonals bisect one another.
- Each diagonal bisects the parallelogram into 2 congruent triangles
- The sum of squares of all the sides of a parallelogram is equal to the sum of the square of its diagonals which is known as the parallelogram law.
What Is Parallelogram Formula?
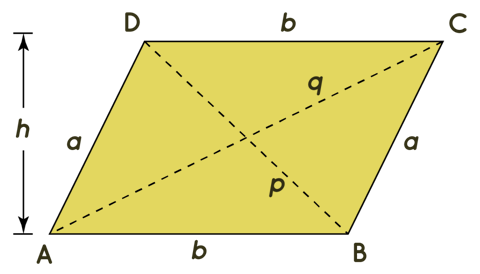
Consider parallelogram ABCD as shown below. Let's understand the Parallelogram Formulas. We have,
- AB || CD, AC || BD
- AB = CD = b
- BC = AD = a
- h = height of the parallelogram
- DB = d1, AC = d2 are digonals of the parallelogram
| Area of Parallelogram | |
|---|---|
| Using Base and Height | A=b*h |
| Using Trignometry | A= abSin(x) |
| Using Diagonal | 1/2 *d1*b2*Sin(y) |
| The perimeter of a Parallelogram | Perimeter=a+b+c+d | Since a=c and b=d | Perimeter= 2a+2b |
|---|
Area of a Parallelogram Formula
A parallelogram's area is the region or surface that a two-dimensional plane occupies. Let's look at how to compute area using the parallelogram formula.
Area of Parallelogram Formula Using Base and Height
- Area of parallelogram formula = Base × Height
- Area of parallelogram ABCD = b × h
- Area of a Parallelogram Formula Without Height
- If the height of the parallelogram is not given, trigonometry can be used to find the area.
- Area of parallelogram formula = a b sin A = b a sin B
Area of a Parallelogram Using Diagonals
The area of any parallelogram can also be calculated using its diagonal lengths. Suppose, the diagonals d1 and d2 intersect each other at an angle of x, then the area of the parallelogram is given by:
- Area of parallelogram formula = ½ ×d1×d1sin(x)
- Area of parallelogram ABCD = ½ × AC × BD sin (x)
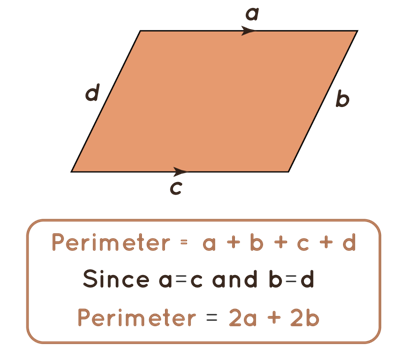
The perimeter of a Parallelogram Formula
The perimeter of a parallelogram is the total distance between the parallelogram's boundaries. The length and width of a parallelogram must be determined before the perimeter can be calculated. Let the parallelogram's sides be a and b. Keeping in mind the parallelogram's feature that the opposite sides are parallel and congruent. The perimeter of a parallelogram is calculated as follows:
- Perimeter = a + b + c + d (when a, b, c, d are representing 4 sides of a parallelogram)
- Since, side AB = CD = b, side BC = AD = a
- Perimeter of a parallelogram = 2 (a+b)
Download all the Maths formulas from the HT maths page.
Find below the pdf for downloading Parallelogram Formula
