All Algebra Formula in One sheet

Find Most Important Algebra Formulas

Algebra is a discipline of mathematics in which letters are used instead of numbers. 

About Algebra Formulas

Algebra is a discipline of mathematics in which letters are used instead of numbers. What is done on one side of the scale with a number is also done on the other side of the scale with the same number. The figures are set in stone. Real numbers, complex numbers, matrices, vectors, and other concepts are all part of algebra. The most widely used letters to express algebraic problems and equations are X, Y, A, and B.

Important Algebraic Formulas

(a+b)2 = a2 + b 2 + 2ab

(a-b)2 = a2 + b 2 - 2ab

a2 - b 2 = (a+b)(a-b)

a2 + b 2 = (a + b)2-2ab

or

a2 + b 2 = (a - b)2+ 2ab

a3 + b 3 = (a + b)(a2- ab + b 2) = (a + b)3 - 3ab(a + b)

a3 - b 3 = (a - b)(a2+ ab + b 2) = (a - b)3 + 3ab(a - b)

2(a2 + b2) = (a + b)2 + (a - b)2

(a + b)2 - (a - b)2 = 4ab

a4 + b4 = (a + b)(a - b)[(a + b)2 - 2ab]

(a - b)2= (a + b)2- 4ab

(a + b)2= (a - b)2+ 4ab

a4 + b4 = [(a + b)2- 2ab]2-2(ab)2

(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

(a + b - c)2=a2 + b2 + c2 + 2ab - 2bc - 2ca

(a - b - c)2=a2 + b2 + c2 - 2ab + 2bc - 2ca

a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 +c2 -ab -bc -ca)

a4 + a2b2+b4 = (a2 + ab + b2)(a2 - ab + b2)

a4+a2 + 1 = (a2 + a + 1)(a2 - a + 1)

if a + b + c = 0 then a3 + b 3 + c3 = 3abc

a8 - b8 = (a4 + b 4)(a2 + b 2)(a + b)(a - b)

Algebra Formulas

Algebra Formulas are the cornerstone of many mathematical concepts. For understanding and solving difficult issues, algebra formulae are used extensively in topics such as equations, quadratic equations, polynomials, coordinate geometry, calculus, trigonometry, and probability. The algebra formulae are useful for completing complex calculations in the shortest amount of time and with the fewest steps possible. The formulas for algebraic expressions are used to simplify algebraic expressions. Let's review what variables, constants, terms, and algebraic expressions are before learning these formulas. A variable is a quantity whose value changes over time and is commonly represented by an alphabet. A constant is a quantity with a set value. A term can be a variable, a constant, or a combination of variables and constants (product or quotient).

The algebraic formulas have also been modified based on the complexity of the math topics. Algebraic formulae exist for topics such as logarithms, indices, exponents, progressions, permutations, and combinations. We'll look at a list of algebraic formulae that are employed in many math topics.

Algebra Formulas

An identity in algebra is a formula that is always true, regardless of the values provided to the variables. For any values of the variables, algebraic identity indicates that the left-hand side of the equation is identical to the right-hand side of the equation. Algebraic identities are used to solve problems with unknown variables. Here are a few of the most common algebraic identities:

Algebraic Identities

  • a2 + 2ab + b2 = (a + b)2
  • a2 - 2ab + b2 = (a - b)2
  • a2 - b2 = (a + b)(a - b)
  • x2 + x(a + b) + ab = (x + a)(x + b)

Examine the algebraic identity (a + b)2 = a2 + 2ab + b2, and see if you can comprehend it in algebra and geometry. Let us try to multiply the statement algebrically and obtain the formula as a proof of this formula. (a + b)2 = (a + 2ab + b 2)

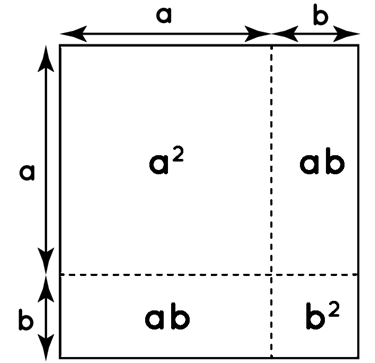
Algebra Formulas

 

(a + b)2 = a 2 + 2ab + b2

 

  • a2 + 2ab + b2 = (a + b)2
  • a2 - 2ab + b2 = (a - b)2
  • a2 - b2 = (a - b) (b+a)
  • a3 + 3a2b + 3ab2 + b3 = (a + b)3
  • (a - b)3 = a3 + 3ab2 - b3- 3a2b
  • a3 + b3 = (a2 - ab + b2) (a + b)
  • a3 - b3 = (a2 + ab + b2) (a - b)
  • (a + b + c)2 = a2 + b2 + c2 + 2bc + 2ca+ 2ab

Exponential laws are further useful to derive some of logarithmic laws

  • am + n = am. an
  • am – n = am/an
  • an = (am)n
  • am. bm = (ab)m
  • a0 = 1
  • a-m = 1/am

xm = a => logx a = m

log a 1 = 0

log a a = 1

log a (xy) = log a x + log a y

log a 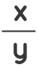Algebraic-formula1 = log a x - log a y

log a (xm) = m log a x

log a x = 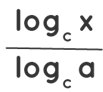Algebraic-formula2

a logox = x

The quadratic equation is written in its general form as ax2 + bx + c = 0, and there are two ways to solve it.

Quadratic Formula

For ax2 + bx + c = 0

Algebraic-formula3

The three sorts of roots are listed below based on the determinant's value

  • If b2 - 4ac > 0, distinct real roots.
  • If b2 - 4ac = 0, equal real roots.
  • If b2 - 4ac < 0, imaginary roots

???????Get the List of Maths formulas. 

Pdf of List of all Important Algebra formulas

All Algebra Formula in One sheet
All Algebra Formula in One sheet

Related Links

Frequently Asked Questions on All Algebra Formula in One sheet

Imporatnt basic math formulas are 

  • a2 - b2 =(a-b)(a+b)
  • (a+b)2 =a2 + 2ab + b2
  • (a-b)2 = a2 - 2ab + b2
  • (x+a)(x+b)=x2 + x(a+b) + ab
  • (a+b+c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
  • (a+b)3 =a3 +3a2b + 3ab2 + b3
  • (a-b)3 =a3 - 3a2b + 3ab2- b3

Algebra in Maths needs lots of practice and it is important too for higher maths, start with memorising Algebra Formulas from the list given on the page. try to understand the derivation before memorising the Algebra Formulas. solve few examples and questions to understand the application of Algebra Formulas.