Sides of Triangle

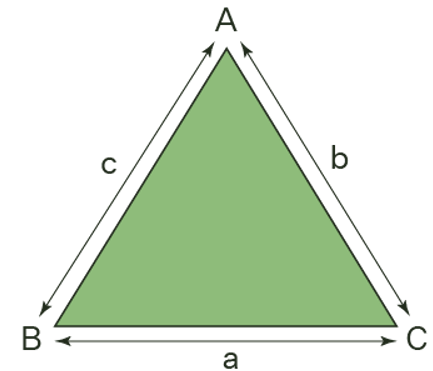
About Sides of Triangle

A triangle's sides are straight lines that are linked by the triangle's three vertices. To put it another way, the sides of a triangle are line segments that intersect at the vertices of the triangle. Sides of a right-angled triangle can be calculated using numerous methods, such as the Pythagoras theorem or the triangle's perimeter. We can use law of cosines or the law of sines to find the lengths of the triangle's sides if some of the angles and other side lengths are known.

In this post, we'll look at the concept of triangle sides and the formula for calculating them. We'll also go through the properties and rules of triangle sides, as well as solve a few cases to help you grasp the topic.

Three sides and three angles make up each triangle. These triangle sides are straight line segments that meet at each vertex of the triangle to produce a closed three-sided figure. Each side of a right-angled triangle is given a name. The hypotenuse is the triangle's longest side; the base is the triangle's lower side, and the perpendicular is the standing line adjacent to the right angle. At each vertex, or end of each side of the triangle, three angles are produced. Let's look at the formula for calculating the lengths of these sides.

Sides of Triangle Formula

The trigonometric ratios are related to the sides of a triangle method for finding its sides. One side of the triangle & an acute angle are required requirements, and we may then determine the remaining triangle sides.

• Right triangle - apply the Pythagorean theorem directly.
• Isosceles triangle - use the area or perimeter formula.

Sides of A Triangle Formula

1. If we are given an angle & a side length for right triangle,
   • Sine θ = Length of opposite side / Length of Hypotenuse side
   • Cos θ = Length of adjacent side / Length of Hypotenuse side
   • Tan θ = Length of opposite side / Length of adjacent side
2. Law of sines: sin(A)/a = sin(B)/b = sin(C)/c
   Where,
   • a, b, & c are sides of the triangles oppo.
   • A, B, & C are corresponding angles.
3. Law of cosines: c² = a² + b²- 2ab cos(C)
   Where,
   • a, b, c are sides of triangles.
   • C is the angle formed by the sides a & b.

Sides of Triangle Properties

Now that we've gone over the formulae for finding the lengths of a triangle's sides, let's go over some of the crucial qualities of triangle sides:

• The longest side of the triangle is the side that is opposite the greatest angle.
• If the lengths of the respective triangle sides are equal, two triangles are said to be congruent.
• If the lengths of the triangle's respective sides are proportional, two triangles are said to be comparable.
• The perimeter of a triangle is equal to the sum of its three sides.
• The area of a triangle can be determined using its three sides (Heron's formula), which is as follows:

Area 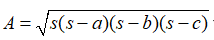where a, b, c are the three sides of a triangle and s is the semi-perimeter.

Sides of Triangle Rule

We've gone through the main qualities of triangle sides so far; now let's look at the basic rule. The rule of the triangle sides states that the total of any two triangle sides is always greater than the length of the third side. The triangle inequality theorem is another name for this condition.

???????Check out the list of Maths formulas prepared by the experts of Home tution.com

Download free pdf of Sides of Triangle Its Use And Solved Examples