Cofactor Formula

About Cofactor Formula

Before going to learn the cofactor formula, let us see where it is used. The inverse of a matrix is used in solving a system of equations. The inverse of a matrix is its adjoint divided by its determinant. The adjoint of the matrix is the transpose of the cofactor matrix. The cofactor matrix is the matrix of the same order as the given matrix where the elements of the original matrix are replaced by their corresponding cofactors. These cofactors are calculated using the cofactor formula. Let us learn the cofactor formula along with a few solved examples. To get all the Maths formulas check out the main page. 

What Is Cofactor Formula?

The cofactorCijof an element a_ijof a square matrix of order n×n is its minorMijmultiplied by(−1)_i+j. Here, the minor M_ijof the elemental is the determinant of the matrix obtained by removing the throw and jth column from the original matrix. i.e.,

Cofactor of an element a_ij is,C_ij=(−1)^i+j⋅M_ij

Here,M_ij= The minor ofa_ij= The determinant of the matrix obtained by removing the throw and jth column.

(i) Minor of a_ij is,

M_ij = Determinant of the matrix obtained by removing the i^th row and J^th column.

(ii) Cofactor of a_ij is,

C_ij = (-1)^{i + j} M_ij

Note:

The determinant of a 2 × 2 matrix 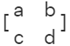is found using the formula,= 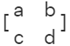ad - bc.

ii) The cofactor of an element can be positive or negative or zero.

Cofactor Formula pdf