About Tan2x Formula
Tan2x is an important trigo function. Tan2x formula is one of the commonly used double angle Trigo formulas and can be represented in terms of different trigo functions such as tan x, cos x, and sin x. As we already know that tan x is the ratio of sin and cos function, hence tan2x identity can also be represented as the ratio of sin 2x and cos 2x. Check out the List of Maths Formulas.
Tan2x is a trigo function and has a formula which is used to solve various problems in trigonometry. Tan2x is an important double angle formula, which is, a trigonometry formula where the angle is doubled. It can be represented in terms of tan x and also as a ratio of sin2x and cos2x. Since the reciprocal of tan x is cot x, therefore we can write tan2x as the reciprocal of cot 2x, which is,tan2x = 1/cot2x. Now take a look at the tan2x formula:
Tan2x Formula
We can write the tan2x formula in two different forms. It can be written in terms of tan function only and as a combination of the sin and cos. The formula for tan2x identity is given as:
tan2x = 2tanx/(1-tan2x)
tan2x = sin2x/cos2x
Tan2x Formula Proof
Here is the derivation of the Tan2x formula. At first, we will use the angle addition formula for tan function to derive the tan2x identity. Note that we can write double angle 2x as 2x = x + x. We will use this concept to prove the formula of tan2x:
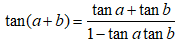
We have
tan2x = tan(x + x)
= (tanx + tanx)/(1- tanx.tanx)
= 2tanx/(1-tan2x)
Therefore, we have derived the tan2x formula by using the angle sum formula of tanfunction.
Download a free pdf of Tan2x Formula Its Use And Solved Examples
