About Central Limit Theorem
Maximum Limit According to the theorem, the probability distribution of arithmetic means from multiple samples drawn from the same population will approximate a normal distribution. The sample size equal to or greater than 30 in order for the central limit theorem to hold.
The average of sample mean & sample standard deviation will resemble the population mean and standard deviation, which is a critical feature of the central limit theorem. We'll study more about the central limit theorem, its formula, proof, applications, and illustrations in this post.
What is Central Limit Theorem?
The central limit theorem states that when numerous samples of a population are taken and their sums are computed, the sums form their own normal distribution. This sum also converges to the population mean due to the law of large numbers. CLT is a common abbreviation for the central limit theorem.
Central Limit Theorem Definition
The central limit theorem asserts that if large enough samples are obtained from the population, the sampling distribution of mean for that random variable will be approximate a normal distribution, regardless of the random variable's distribution. This is valid for samples with a number larger than or equal to 30. As more large samples are collected, the sample mean graph begins to resemble a normal distribution.
Central Limit Theorem Example
Example:The sample mean values for a group of samples taken from a bigger sample are 12, 10, 11, 14, 12, 13, 15, 9, 12 Calculate the population average.
Solution: Sample mean values 12, 10, 11, 14, 12, 13, 15, 9, 12 The population mean values are average of the above sample mean values
μ=12, 10, 11, 14, 12, 13, 15, 9, 12 /9
=12
Answer:Hence, the population mean is 12
Central Limit Thm Formula

Suppose there is a random variable, X, with an unknown or a known probability distribution. Letσ be the standard deviation andμbe the mean of X. If a large number of samples are drawn of size n then according to the central limit theorem formula, the new random variable,X¯, consisting of the sample means, will be normally distributed. This is given as:
¯¯¯X∼N(μ, σ/√n)
Thus, the central limit formula says that the random variable of the sample means be normally distributed with mean that will be equal to the original distribution With mean that will be equal to the original distribution & and standard deviationgiven by σ / √n.
z score for random variable,¯¯¯¯x¯, is given as follows:
z=¯x−μ / σ√nz
where,¯¯¯x is the mean ofX¯
μandσare the mean and standard deviation of X respectively.
Central Limit Theorem Proof
Let us suppose we haveX1,X2, ...Xn independent and identically distributed random variables with varianceσσ= 1and meanμ= 0.
Let M(t) be the moment generating function of each xi.
M(0) = 1
M'(1) = E[Xi] =μ= 0
M''(0) = E[X2i] = 1
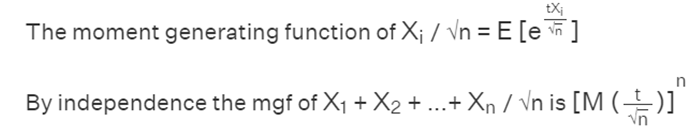
Let L(t) = log M(t)
L(0) = log M(0) = 0
L'(0) = M'(0) / M(0) =μ/ 1 =μ
L''(0) = M(0)M″(0)− M′(0)^2 / M′(0)^2 = 1
Using the L'Hospital Rule we find t / √n as t2/ 2
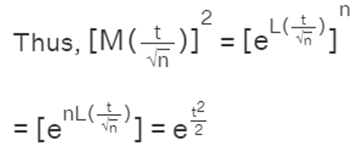
This is the moment generating function of standard normal distribution, thus proving the central limit theorem.
Central Limit Theorem Application
The central limit theorem is commonly employed in situations when it is necessary to identify population features but examining the entire population is problematic. The central limit theorem is also used in the following applications.
- In data science, the central limit theorem is used to make accurate assumptions of the population in order to build a robust statistical model.
- The CLT is used in applied machine learning to make conclusions about model performance.
- The central limit theorem is used in statistical hypothesis testing to determine whether a given sample belongs to a specific population.
Related Articles:
- Online Normal Distribution Calculator
- Probability and Statistics
- Data
Important Notes on Central Limit Theorem
- According to the central limit theorem, if the sample sizes are large enough, the sampling distribution of the means will resemble a normal distribution.
- According to the CLT, the sample mean will be the same as the population mean..
- The sample standard deviation is given by using the central limit theorem. (Population standard deviation) / √n.
- The z score formula is as follows.
To get all the Maths formulas check out the main page.
Find pdf of the Central Limit Theorem example
Frequently Asked Questions
The Central Limit Theorem (CLT) states that the distribution of the sample mean of a sufficiently large random sample from any population approaches a normal distribution, regardless of the original population's distribution. This theorem is crucial in statistics as it allows for the use of normal probability models in hypothesis testing and confidence intervals.
The CLT is widely used in fields like finance, economics, and quality control. It helps in predicting stock market trends, analyzing survey results, and ensuring accurate estimations in manufacturing processes.