Diagonal of The Rectangle

Before we get into the formula for the diagonal of a rectangle, let's define the diagonal of a rectangle. A rectangle's diagonal is a line segment which connects any two of its non-adjacent vertices. When the rectangle's dimensions are known, the formula for the diagonal of a rectangle yields the length of the diagonal. Let's look at the diagonal of a rectangle formula and solve a few problems.

Diagonal of the rectangle formula

A line segment which connects any two of its non-adjacent vertices of a rectangle is called it's diagonal. AC and BD are diagonal in the given figure. As you can see, the lengths of AC and BD are identical. A diagonal divides a rectangle into two equal right triangles with sides equal to the rectangle's sides and a hypotenuse. The diagonal is the hypotenuse. The diagonals in the following rectangle are AC and BD. Both AC and BD have the same lengths. You can get all Maths formulas on one-page visit the Maths Formulas section of HT.

The length of diagonals can be calculated as,

$d = \sqrt{(I^{2} + w^{2})}$

Where,

l = length of the rectangle

w = width of the rectangle

Derivation Diagonal of The Rectangle

Using the Pythagoras theorem we can derive the formula for the diagonal of the rectangle. Let us consider a rectangle ABCD of length "l" and width "w". The length of each diagonal is "d".

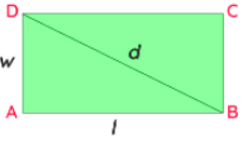
Derivative formula

By using the Pythagoras theorem in triangle ABD,

^{$d^{2} = (I^{2} + w^{2})$}

Taking square root on both sides,

$d = \sqrt{(I^{2} + w^{2})}$

Thus, the diagonal of a rectangle can be mathematically written as:

$d = \sqrt{(I^{2} + w^{2})}$

Where,

l = length of the rectangle
w = width of the rectangle

Diagonal of The Rectangle