About Fibonacci Sequence Formula
Setting F0 = 0, F1 = 1, and using the formula below to determine Fn, the Fibonacci sequence formula for "Fn" is defined using the recursive formula. The Fibonacci formula can be found here. Fn = Fn-1 + Fn-2, where n > 1
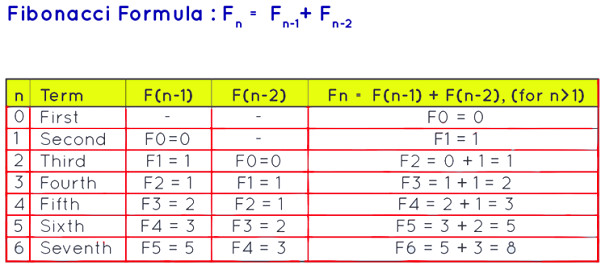
It's worth noting that F0 is the first phrase here (but NOT F1).
Properties of Fibonacci Sequence The Fibonacci sequence has the following intriguing properties:
| A | B | A/B |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6 |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 144 | 233 | 1.618055555555556 |
| 233 | 377 | 1.618025751072961 |
- The golden ratio is connected to Fibonacci numbers. The golden ratio can be used to calculate any Fibonacci number, Fn =(Φn - (1-Φ)n)/√5, φ is golden ratio and Φ ≈ 1.618034. find 7th term, we apply F7 = [(1.618034)7 - (1-1.618034)7] / √5 = 13
- The "golden ratio" is the ratio of successive Fibonacci numbers. Let A and B be the Fibonacci sequence's two consecutive numbers. B/A thus approaches the Golden Ratio. We may use the formula above to discover any term in the Fibonacci sequence.
- The approximated Fibonacci number is obtained by multiplying the preceding Fibonacci number by the golden ratio (1.618034). 13 is a number in the sequence, for example, and 13 × 1.618034... = 21.034442. The next Fibonacci number after 13 in the sequence is 21.
- A multiple of n is every nth number. Examine the series for another pattern of interest. Every third number in the sequence is a two-digit multiple. Every fourth number is a multiple of three, and every fifth number is a multiple of five.
- The Fibonacci sequence can also be used below zero. F-n = (-1)n+1 Fn is the formula. For instance, F-4 = (-1)5. F4 = (-1)3 = -3.
- The sum of n terms of Fibonacci Sequence is given by Σi = 0n Fi = Fn+2 - F2 (or) Fn+2 - 1, where Fn is the nth Fibonacci number. (Note: the first term starts from F0)
For example, the sum of first 10 terms of sequence = 12th term - 1 = 89 - 1 = 88. It can be mathematically written as Σi=09 Fi = F11- 1 = 89 - 1 = 88.
