About Scalene Triangle
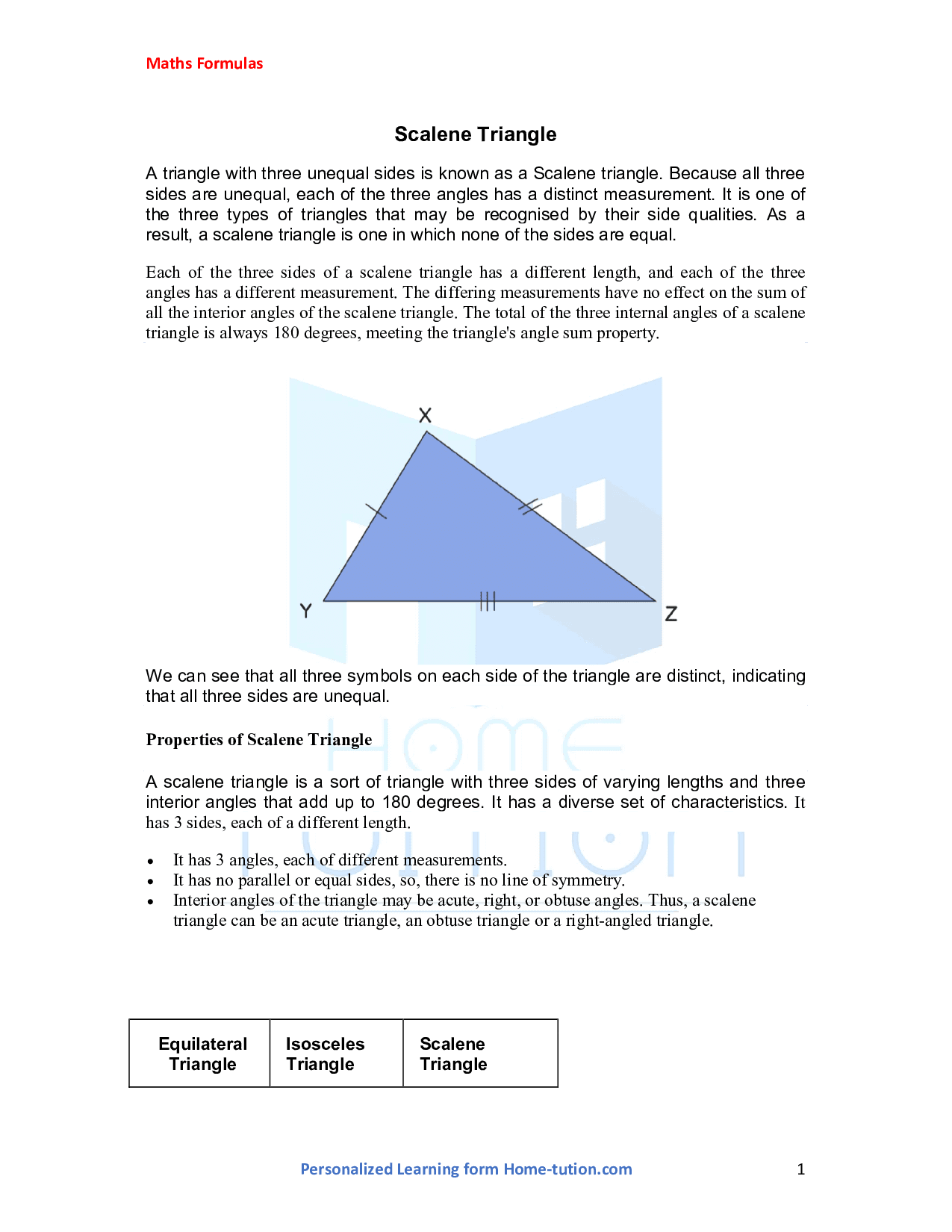
A triangle with three unequal sides is known as a Scalene triangle. Because all three sides are unequal, each of the three angles has a distinct measurement. It is one of the three types of triangles that may be recognised by their side qualities. As a result, a scalene triangle is one in which none of the sides are equal.
Each of the three sides of a scalene triangle has a different length, and each of the three angles has a different measurement. The differing measurements have no effect on the sum of all the interior angles of the scalene triangle. The total of the three internal angles of a scalene triangle is always 180 degrees, meeting the triangle's angle sum property.
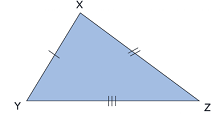
We can see that all three symbols on each side of the triangle are distinct, indicating that all three sides are unequal.
Properties of Scalene Triangle
A scalene triangle is a sort of triangle with three sides of varying lengths and three interior angles that add up to 180 degrees. It has a diverse set of characteristics. It has 3 sides, each of a different length.
- It has 3 angles, each of different measurements.
- It has no parallel or equal sides, so, there is no line of symmetry.
- Interior angles of the triangle may be acute, right, or obtuse angles. Thus, a scalene triangle can be an acute triangle, an obtuse triangle or a right-angled triangle.
| Equilateral Triangle | Isosceles Triangle | Scalene Triangle |
|---|---|---|
| When all the 3 sides of the triangles are equal in length, it is an equilateral triangle. | When any 2 sides of the triangle are equal in length, it is an isosceles triangle. | When all the 3 sides of triangle are of different measures, it is a scalene triangle. |
| In an equilateral triangle, all three angles are identical in size. Each angle is 60 degrees. | The angles opposing the equal sides are equal in an isosceles triangle (Isosceles Triangle Theorem) | All three angles in a scalene triangle have distinct measurements. |
- Scalene Triangle Formula
- The Perimeter of a Scalene Triangle and the Area of a Scalene Triangle are the two main formulas for a scalene triangle.
- Perimeter of a Scalene Triangle
- A triangle's perimeter is equal to the total of its three sides, or (a + b + c) units. The perimeter of the scalene triangle is thus (a + b + c) units, where a, b, and c signify the scalene triangle's three sides.
- Area of a Scalene Triangle
- Area of the triangle =(1/2) × b × h square units
- “b” refers to base of triangle
- “h” refers to height of triangle
- If the height and base of the triangle are unknown, but the sides are, we can use Heron's formula. Thus, The scalene triangle's area
- A = square units.
- We can apply Heron's formula if the triangle's height and base are unknown but the sides are. Thus, The area of the scalene triangle
- Important Notes
- A scalene triangle is made up of three sides, each of which is variable in length, and three angles, each of which is distinct in size.
- It also adheres to the triangle's angle sum property.
- A scalene triangle lacks symmetry because the lengths of the sides are varied and even angles are measured differently.
Download all the Maths formulas from the HT maths page.
Find below the pdf for downloading Scalene Triangle Formula
