About Taylor Series Formula
A function's Taylor series is an infinite sum of terms written in terms of the function's derivatives at any one point, with each subsequent term having a bigger exponent such as x, x2, x3, and so on. The Taylor series formula aids in the depiction of the Taylor series mathematically. Let's look at the Taylor series formula with some examples at the bottom of the page. Check out the List of Maths Formulas.
Using the derivatives of a function, the Taylor series formula can be used to expand a function around a variable value. It can be expressed as follows:
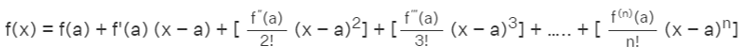
OR,
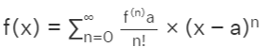
Here,
- f(x) = Real or complex-valued function, that is infinitely differentiable at real or complex number "a" is the power series
- n = Total number of terms in series
Taylor's Series Theorem Statement:
Assume that if f(x)f(x) be a real or composite function, which is a differentiable function of a neighbourhood number that is also real or composite. Then, the Taylor series describes the following power series:
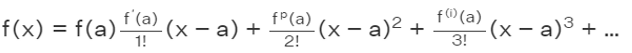
In terms of sigma notation, the Taylor series can be written as
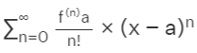
Where,
f(n)(a)=nth derivative of f
n! = factorial of n