About Angles Formulas
Angle formulas are used to calculate angle measurements. Two intersecting rays, known as the angle's arms, share a common terminus to form an angle. T
Angle formulas are used to calculate angle measurements. Two intersecting rays, known as the angle's arms, share a common terminus to form an angle. The vertex of the angle refers to the angle's corner point. The angle is the amount of rotation between the two lines. Angles are measured in radians or degrees.
What Are Angle Formulas?
The angle formulas for the angle created at the centre of the circle by two radii and the arc have been explored here. Let's look at the formulas for numerous angles and double angles in trigonometry as well.
Multiple Angle Formulas
Trigonometric functions frequently contain numerous angles. Multiple angle values cannot be directly found, but they can be calculated by expressing each trigonometric function in its extended form. The Eulers formula and the Binomial Theorem are used to calculate numerous angles of the type sin nx, cos nx, and tan nx that are stated in terms of sin x and cos x alone. In mathematics, the following many angle formula identities are employed.
Formula 1: The sin formula for multiple angles is:
Sin nθ =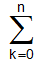 
coskθ sinn-kθ Sin[1/2(n-k)]π
where n = 1,2,3,.........
Sin2θ = 2 Cosθ.Sinθ,Sin3θ = 3Sinθ - 4Sin3θ
Formula 2:The multiple angle’s Cosine formula is given below:
Cos nθ = 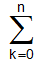CoskθSinn-kθ Cos[12(n - k)]π
Where n = 1,2,3.....................
Cos2θ = Cos2θ.Sin2θ,Cos3θ = 4Cos3θ - 3Cosθ
Formula 3:Tangent Multiple Angles Formula
tan nθ = Sin nθ/Cos nθ
Where n = 1,2,3 ........
Double Angle Formulas
The trigonometric ratios of double angles (2) are expressed in terms of trigonometric ratios of single angles () using Double Angle Formulas. The Pythagorean identities are used to derive some alternative formulas. The double angle formulas are particular cases of (and so derived from) the sum formulas of trigonometry. By substituting A = B in each previous sum formula, we get the double angle formulas for sin, cos, and tan. In addition, we develop various alternative formulas utilising Pythagorean identities.
Double angle formulas of sin, cos, and tan are
sin 2A = 2 sinA cosA(or)(2tanA)/(1+tan2A)
sin 2A = cos2A - sin2A (or)2cos2A - 1(or)1 - 2sin2A(or)(1 - tan2A)/(1 + tan2A)
tan 2A = (2 tan A) / (1 - tan2A)
What is Central Angle of Circle Formula?
The central angle of a circle formula determines the angle formed by two circle radii. A central angle is defined as the angle formed by the arc of a circle and the two radii at the circle's centre. The arms of the central angle are formed by the radius vectors. The arc length that subtends the central angle at the centre and the radius of the circle are needed to compute the central angle. The formula for calculating a circle's central angle is as follows:
Central angle, θ = (Arc length × 360º)/(2πr) degrees or
Central angle, θ = Arc length/r radians, where r is the radius of the circle.
To get all the Maths formulas check out the main page.
Find the pdf of Are Angle Formulas
Frequently Asked Questions
Angles formulas are crucial in trigonometry for solving triangles, calculating distances, and engineering designs. They are widely used in navigation, architecture, physics, and even in computer graphics for 3D modeling.
To memorize angle formulas easily, use mnemonic techniques, practice with real-world examples, and apply formulas in problem-solving regularly. Flashcards and visual diagrams also help in quick recall.
The essential angles formulas in geometry include the sum of interior angles of a polygon (n−2)×180. exterior angle theorem, and trigonometric angle identities such as sin(θ)=opposite/hypotenuse