About Diagonal of a Cube Formula
The diagonal of a cube formula is used to calculate the lengths of the cube's various diagonals, such as the face and body diagonals. A cube is a three-dimensional solid shape, commonly known as a square solid, with all edges measuring the same. This means that a cube's length, width, and height are all the same, and each face is a square. Let's look at some examples of the diagonal of a cube and the diagonal of a cube formula for calculating the lengths of the face and body diagonals. You can get all Maths formulas on one-page visit the Maths Formulas section of HT.
What is the diagonal of a cube?
A cube's diagonal is the line segment that links any two non-adjacent cube vertices. Because this 3D shape contains all 12 equal edges and is one of the most regularly seen shapes around us, the cube is one of the most essential geometric shapes. Ice cubes, sugar cubes, Rubik's cubes, and playing dice are all instances of cubes in real life.
Body diagonal of a cube
The body diagonals run through the cube's body, connecting the opposite vertices. As a result, a cube has four body diagonals that cross through it and connect the opposite corners.
Diagonal of cube Formula
The length of a cube's diagonals can be estimated using the parameters and requirements provided.
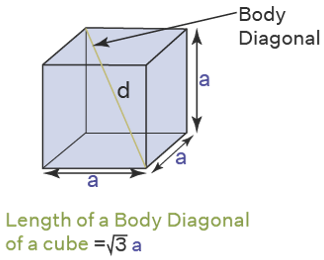
Length of body diagonal of a cube
The length of a space or body diagonal of a cube is calculated using the formula Length of each body diagonal of a cube = √3a, where a is the length of each side of a cube.
Derivation of diagonal of a cube formula
The body diagonal of the cube is commonly referred to by the diagonal of a cube formula. The Pythagoras theorem can be used to derive this formula. Consider the cube's side as 'a,' the face diagonal as r, and the body diagonal as d. When the face diagonal and the body diagonal are joined, a right-angled triangle with sides a, r, and d is produced. The hypotenuse of the right-angled triangle that is formed is the body diagonal.
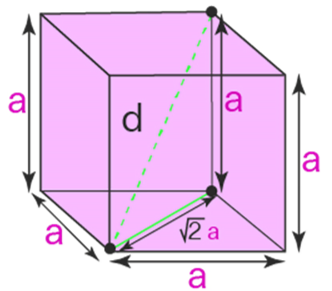
The Pythagorean theorem gives us a2 + r2 = d2 (equation 1)
Because we now know that the face diagonal is √2a (using Pythagoras theorem in the bottom square face), we may substitute 'r' with √2a, making 'r' = √2a.
We get the following by replacing the value of r in equation 1.
a2 + (√2a)2= d2
a2 + 2a2 = d2
3a2 = d2
d = √ (3a2)
d = √3a
As a result, the cube diagonal formula = √3a
Download the pdf of Diagonal of a Cube Formula
