Interquartile Range(IQR) Formula

About Interquartile Range(IQR) Formula

The formula for calculating the difference between the third and first quartiles is known as the interquartile range formula. The interquartile range formula divides an ordered collection of data into quartiles to calculate variability. The first, second, and third quartiles, represented by Q₁, Q₂, and Q₃, respectively, are three values or cuts that divide each respective component.

• Q₁ is cut in the first half of the rank-ordered data set
• Q₂ is the median value of the set
• Q₃ is cut in the second half of the rank-ordered data set.

The Interquartile Range (IQR) formula is a measure of a data set's middle 50%. The Interquartile Range is the smallest of all statistical measures of dispersion. The interquartile range is the difference between the upper and lower quartiles.

IQR Formula

• Upper Quartile – Lower Quartile = Interquartile range
• Q₂ = Q₃ – Q₁
• where,
• IQR = Interquartile range (IQR = Q₂ = Q₃ - Q₁)
• Q₁ = (1/4)[(n + 1)]^th term)
• Q₃ = (3/4)[(n + 1)]^th term)
• n = number of data points

IQR = Q₂ = Q₃ - Q₁

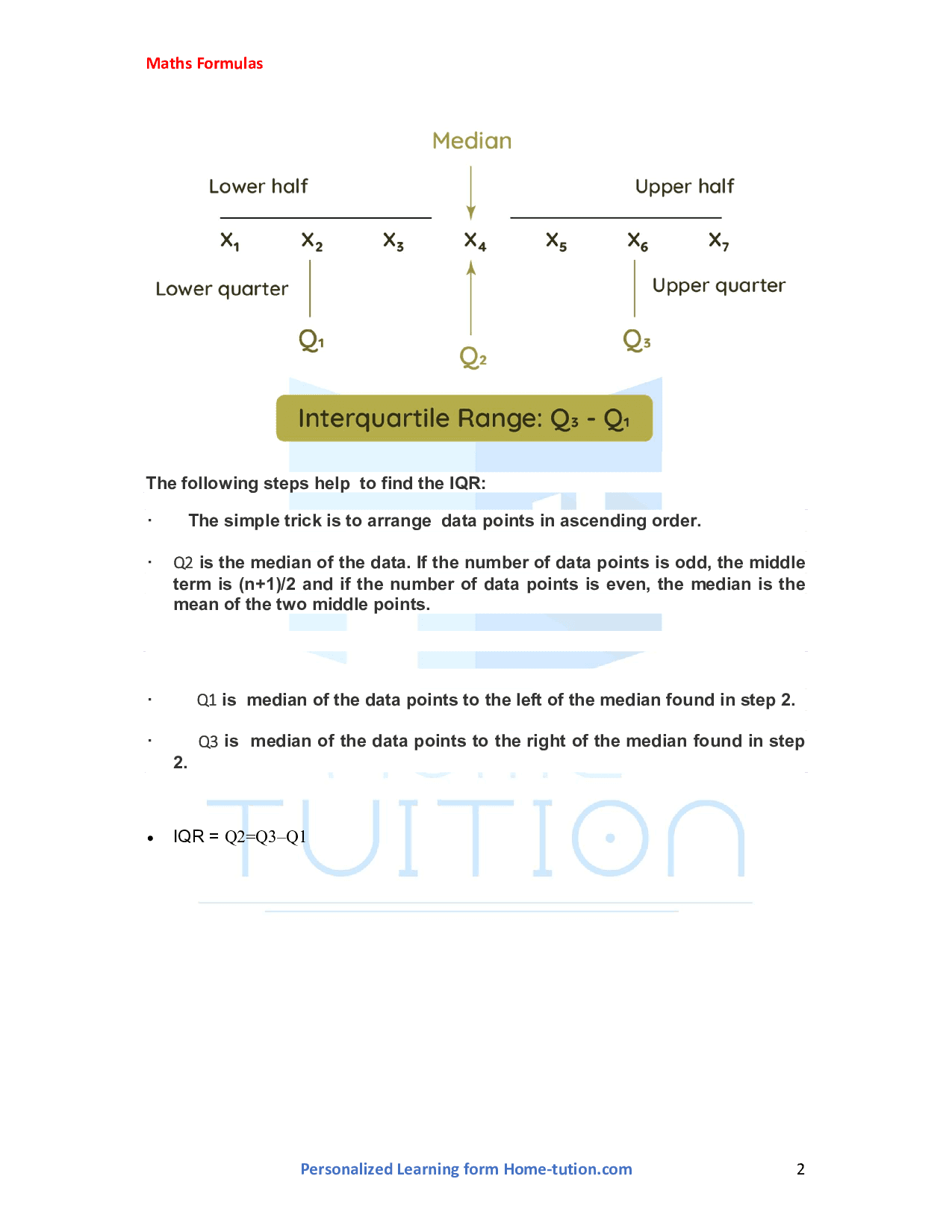
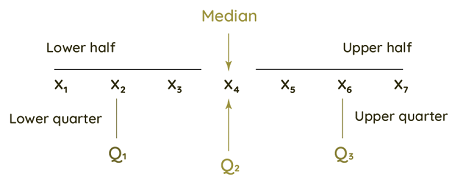
• The following steps help to find the IQR:
• The simple trick is to arrange data points in ascending order.
  1. Q₂ is the median of the data. If the number of data points is odd, the middle term is (n+1)/2 and if the number of data points is even, the median is the mean of the two middle points.
  2. Q₁ is the median of the data points to the left of the median found in step 2.
  3. Q₃ is the median of the data points to the right of the median found in step 2.
  4. IQR = Q₂ = Q₃ - Q₁

Get a List of all Maths Formulas on one page.

Download the pdf of Interquartile Range(IQR) Formula