About the area of Octagon
The area of an octagon is defined as the entire area contained by all of the octagon's octa(eight) sides. An eight-sided polygon is called an octagon. By dividing the octagon into eight equal isosceles triangles, the area may be determined. We'll go over the octagon's area in depth in this mini-lesson. For more Maths formulas click on the main page.
What is the Area of the Octagon?
The area of an octagon is the space between its eight sides, and it is a two-dimensional form having eight sides. We can use the area of an isosceles triangle to compute the octagon's area. We determine the area of the shape by dividing it into eight equal isosceles triangles. The lengths of the sides of a regular octagon are equal, as are the angles between them. Each inside angle is 135 degrees, while each outer angle is 45 degrees.
Area of Octagon Formula
The general formula we use to calculate the area of the octagon is: 2s2(1+√2), where s is the length side of the octagon.
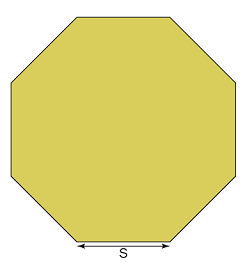
How to Calculate Area of Octagon?
The area of an octagon is 2s2(1+√2). By using the following steps mentioned below we can find the area of the octagon.
Solved Example of the area of an octagon
Q-1 If the sum of interior angles of a polygon is 1080°, then this is a
(a) pentagon.
(b) hexagon.
(c) octagon.
(d) nonagon.
Ans. (c)
Explanation:
Sum of interior angles of a polygon with n sides = (n-2) x 180°.
Therefore,1080° = (n-2) x 180°
n = 8
Thus, the required polygon will be an octagon.
Q-2 The sum of the interior angles of an octagon is
(a) 1080°.
(b) 900°.
(c) 720°.
(d) 360°.
Ans. (a)
Explanation:
By dividing the octagon into triangles, we get six triangles.
So, the sum of interior angles of an octagon is
6 x 180° = 1080° (Sum of angles of a triangle is 180°)
Download pdf of definition and solved example of Area of Octagon
