About a2-b2 Formula
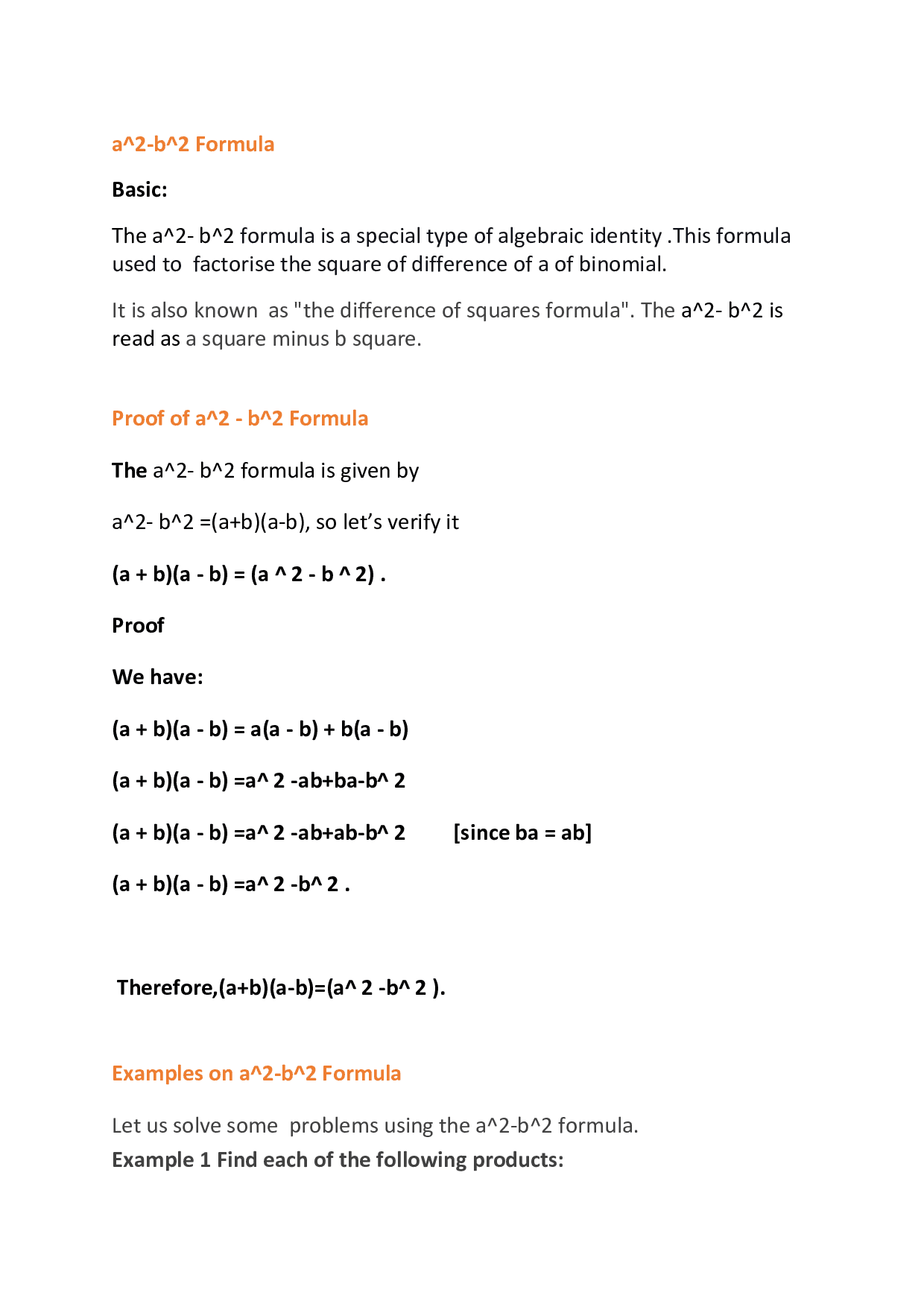
The a2- b2 formula is a special type of algebraic identity. This formula is used to factorise the square of the difference of a binomial.
It is also known as "the difference of squares formula".The a2- b2 is read as a square minus b square. More Maths Formulas on the parent's page.
Proof of a2 - b2 Formula
- The a2- b2 formula is given by
- a2- b2 =(a+b)(a-b), so let’s verify it
- (a + b)(a - b) = (a2 - b2) .???????
- Proof
- We have:
- (a + b)(a - b) = a(a - b) + b(a - b)
- (a + b)(a - b) =a2 -ab+ba-b2
- (a + b)(a - b) =a2 -ab+ab-b2 [since ba = ab]
- (a + b)(a - b) =a2 -b2 .
- Therefore,(a+b)(a-b)=(a2 -b2 ).
Solved Examples on a2-b2 Formula
Let us solve some problems using the a2-b2 formula.
- Example 1 Find each of the following products:
- (4x + 5y)(4x - 5y)
- Solution
- We have:
- Using (a+b)(a-b)=(a2 -b2 )
- (4x + 5y)(4x - 5y)
- = (4x) 2 - (5y) 2
- =(16x2-25y2 )
- Example 2:Factorise(x³ - x)
- SOLUTION
- We have
- (i) (x³ − x) = x(x² − 1)
- = x(x-1)(x + 1)
- [Using (a²-b²) = (a−b)(a + b)]
- (x³-x) = x(x-1)(x+1).
- Example 3:Simplify 152- 52usinga2-b2formula
- Solution:To find152- 52
- Let us assume a = 15 and b = 5
- Using formulaa2- b2= (a - b) (a+ b)
- 152-52= (15 - 5) (15 + 5)
- = 15(15 +5) - 5(15 + 5)
- = 225+75 -75 -25
- Answer:152-52= 200
- Example 4: Factorise x ^ 2 - 1 - 2a - a ^ 2
- SOLUTION
- We have
- x 2 - 1 - 2a - a 2
- =x2-(1+2a+a2 )
- =x2 -(1+a)2
- [Using (a²-b²) = (a−b)(a + b)]
- =(x-1-a)(x+1+ a) .
- Therefore, (x 2 - 1 - 2a - a 2) = (x - 1 - a)(x + 1 + a)
Identity: An identity is equality which is true for all values of the variable(s).
Standard identities
Identity 1 : (a + b)2 = a2 + 2ab + b2
Identity 2 : (a – b)2 = a2 – 2ab + b2
Identity 3 : (a + b) (a – b) = a2 – b2
Identity 4 : (x + a) (x + b) = x2 + (a + b) x + ab
Identity 5 : (a + b + c)2 = (a2 + b2 + c2) + 2(ab + bc + ca)
Identity 6 : (a + b – c)2 = (a2 + b2 + c2) + 2(ab – bc - ca)
Identity 7 : (a + b)3 = a3 + b3 + 3ab (a + b)
Identity 8 : (a - b)3 = a3 – b3 – 3ab (a – b)