About Average Rate of Change Formula
Average Rate of Change Formula The average rate of change refers to the rate at which one quantity changes in relation to another. It indicates how much the function changed per unit throughout the specified time interval. Simply put, the rate of change is the difference between the amount of change in one item and the comparable amount of change in another. Let's take a closer look at the average rate of change formula.
What is the Average Rate of Change?
The ratio of "change in the function values" to "change in the interval endpoints" is the average rate of change of a function f(x) over an interval [a, b]. i.e., [f(b) - f(a)] / (b - a). In other terms, the "ratio of change in outputs to change in inputs" is the average rate of change (denoted by A(x)). i.e.,
A(x)=
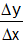
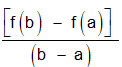
Changes in y-values (or function values) are represented by y, and changes in x-values (or interval endpoints) are represented by x. The following are some instances of average rates of change:
A bus moves at 80 kilometres per hour.
A lake's fish population grows at a rate of 100 each week.
When the voltage in an electrical circuit drops by one volt, the current in the circuit drops by 0.2 amperes.
The formula for the Average Rate of Change
The average rate of change function describes the average rate of change of one quantity in relation to another quantity. The formula for calculating the average rate of change is as follows:
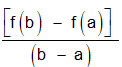
where,
A(x) = Average change rate
f(a) = Function f(x) value at a
f(b) = Function f(x) value at b
Solved Example of Average Rate of Change Formula
Example: Calculate the average rate of change of f(x) = 2x + 10 as x increases from 3 to 7.
Sol:
f(x) = 2x + 10, a = 3, b = 7.
f(3) = 2(3) + 10 = 6 + 10 = 16
f(7) = 2(7) + 10 = 14 + 10 = 24
By using the average rate of change formula,
A(x) = [f(b)−f(a)] / (b−a)
A(x) = [f(7)−f(3)]/ (7−3)
A(x) = (24 - 16) / 4
A(x) = 8/4
A(x) = 2
Thus, the rate of change is 2.
To get all the Maths formulas check out the main page.

