Radical

About Radical

A radical is the inverse of an exponent, which is represented by a symbol ", also known as the root, in mathematics. It can be a square or cube root, with the number preceding the sign or radical serving as an index number or degree. This is a whole number that cancels out the radical when expressed as an exponent.

What do you mean by Radical?

Radical and root of a number are the same thing. The root can be a square root, a cube root, or an nth root in general. As a result, a radical is any number or phrase that uses a root. The word "radical" comes from the Latin word "radix," which meaning "root." The radical can be used to explain several types of roots for a number, such as square, cube, fourth, and so on. The index number or degree is the number written before the radical. This number indicates how many times the radicand must be multiplied by itself to equal the number.

Example: ?(125) = 5 as 5 × 5 × 5 = 125.

Definition of Radical

The symbol ‘Ö’ for a number's root is known as radical, and it is written as x radical n or nth root of x. The vinculum is the horizontal line that surrounds the number, and the radicand is the number beneath it. The index or degree is the number n written before the radical. Some examples of radicals are √7, √2y+1, etc.

The following terms can also be used to describe a radical:

1. A radical equation is an equation that lies inside a radical.
2. A radical expression is an expression that lies inside a square root.
3. Radical inequality is an inequation that exists within a radical.

Radical General Rules

A few general guidelines for radicals are shown below.

Example, √x = 25 => (√x)²= (25)²=> x = 625.

The radical itself is equal to the index number's inverse exponent. Example, √7 = (7)^1/2.

Radical Formula

A radical equation must be made radical-free before it can be solved. We power both sides of the equation with 'n' to make an equation of nth root radical free. This obscured the radical equation, which was free of radicals.

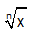=p

x^(1/n)= p

x^(1/n)n= pⁿ

x = pⁿ

Here, The 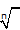symbol is known as the radical of nthroot, 'n' is known as the index.

The expression or variable inside the radical symbol i.e, x is known as the radicand.

1. The outcome will be positive if the number is positive under the radical.
2. The outcome will be negative if the number under the radical is negative.
3. The outcome will be an irrational number if the number under the radical is negative and the index is an even integer.
4. The radical will be square root if no index is specified.
5. It is possible to multiply numbers with the same radical and index. Example, ?12 × ?10 = ?120.
6. For numbers with the same radical, division is possible. Example, √8/√4 = √(8/4) = √2.
7. The number can be split under the same radical in the reverse of the multiplication rule. Example, √27 = √9 × √3 = 3 × √3.
8. In any equation, the radical can also be represented in its exponent form.

Download free pdf of Radical Formulas Its Use And Solved Examples