About Exponential Distribution
The exponential distribution is defined as a probability distribution of time between occurrences in the Poisson point process in probability theory. The exponential distribution is thought to be a subset of the gamma distribution. In addition, the exponential distribution is the geometric distribution's continuous analogue.
What do you mean by Exponential Distribution?
The exponential distribution is a continuous probability distribution in probability theory and statistics that often concerns the amount of time until a given event occurs. It is a process in which events occur at a constant average rate, continuously and independently. The key attribute of the exponential distribution is that it is memoryless. More little values or fewer larger variables can make up the exponential random variable. The quantity of money spent by a customer at the supermarket, for example, follows an exponential distribution.
The formula for Exponential Distribution
If a continuous random variable, say X, has the following probability density function, it is said to have an exponential distribution:
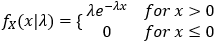
Here λ is called the distribution rate.
Exponential Distribution Mean and Variance Mean:
The exponential distribution's mean is calculated using parts integration.
Mean = E[X] =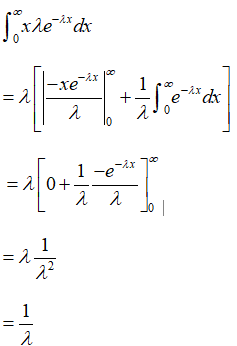
Thus, the mean of exponential distribution = 1/λ
To calculate the variance of an exponential distribution, we must first determine the second moment of the distribution, which is given by:
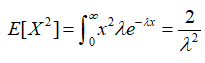
Thus, the variance of a continuous random variable, X is calculated as:
Var (X) = E(X2)- E(X)2
Now, substituting the value of the mean and second moment of the exponential distribution, we get,
Var (X) =