Inverse Variation Formula

About Inverse Variation Formula

• Inverse variation occurs when one quantity declines while the other grows, or vice versa. This means that if one quantity's size or absolute value falls, the product will always remain the same. The proportionality constant is another name for this product.
• An inverse relationship between two quantities is represented by inverse variation. Inverse variation has various practical applications. For example, as a car's speed increases, the time it takes to arrive to its destination decreases. We'll go through inverse variation, its formula, graph, and some instances in this post.
• What is Inverse Variation?
• Inverse variation establishes proportionality between two inversely related quantities. Proportionalities are divided into two categories. Direct variation and inverse variation are the two types. If an increase or decrease in one of the quantity causes a comparable rise or decrease in the other, the two quantities are said to be directly proportional. In contrast, an inverse variation occurs when one quantity grows while the other decreases.
• Inverse Variation Definition
• If the product of 2 non-zero numbers provides a constant term, then they are said to be in inverse variation (constant of proportionality). In other words, if one number is directly proportional to the reciprocal of the other, the two quantities follow inverse variation. This indicates that increasing one quantity causes the other to decrease, while decreasing one quantity causes the other to rise.

• Inverse Variation Formula
• To demonstrate proportionality, the sign "∝" is used. If two variables x and y have the same inverse variation, they are represented as follows:
  • x ∝ 1/y or y ∝ 1/x
  • A constant/proportionality coefficient must be included to convert this expression into an equation. As a result, the inverse variation formula is as follows:
  • x = k/y or y = k/x
  • xy = k
  • Here, k is the constant of proportionality. Also, x ≠ 0 and y ≠ 0
• Product Rule for Inverse Variation
  • Suppose the two solutions of inverse variation are (x1 x1, y1 y1) and (x2, y2).
  • This can also be expressed as x1 y1 = k and x2 y2 = k.
  • Using these two equations,
  • x1 y1 = x2 y2 or x1/x2 = y2/y1
  • This is the product rule for inverse variation.

  Inverse Variation Graph

  • A rectangular hyperbola is the graph of an inverse variation. If two inversely varying values x and y are multiplied together, their product equals a constant k. The graph never crosses the x-axis or the y-axis since neither x nor y can be equal to zero. The following is the graph of an inverse variation with the function y = k / x:
  • 

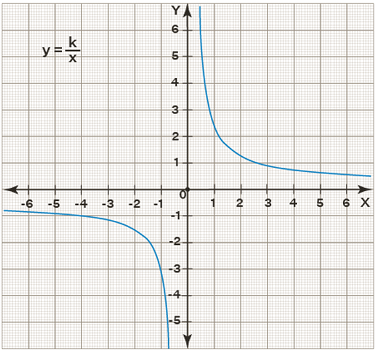
  Inverse Variation Table

  • An inverse variation table is used to look at how one quantity varies when another changes in an inverse proportional relationship. Assume that y = 24 / x is the inverse variation of two values x and y. The inverse variation table then looks like this:

  x	y = 24/x
  1	24
  2	12
  3	8
  -3	-8
  -2	-12
  -1	-24

  Important Notes on Inverse Variation
  • Both quantities are said to exhibit an inverse variation if one drops while the other increases and vice versa.
  • An inverse variation is represented as x ∝ 1/y or x = k/y.
  • If one decreases while the other increases, the two quantities are said to have inverse variation.
  • A rectangular hyperbola in the cartesian coordinate plane will come from two values undergoing an inverse variation.

Get a List of all Maths Formulas on one page.

Download the pdf of Inverse Variation