Baye's Formula

About Baye's Formula

p(a/b)= p(b / a)p(a)/p(b)

Bayes Theorem Statement

Let E1, E2,..., En represent a set of events associated with a sample space S, where all E1, E2,..., En events have a nonzero probability of occurrence and constitute a partition of S. If A is any event related to S, then Bayes theorem says that

P(E_i|A)=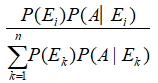

for any k = 1, 2, 3, …., n

Bayes Theorem Proof

According to the conditional probability formula,

P(E_i|A)=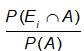---------------(1)

Using the multiplication rule of probability,

p(E_i ∩ A) = p(E_i)p(A|E_i)----------------(2)

Using total probability theorem

p(A) = 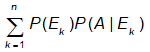---------------(3)

On putting the values from equations (2) and (3) in equation (1), we have

P(E_i|A)=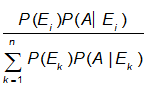---------------(1)

Bayes Theorem Formula

If A and B are two separate events, then the formula for Bayes theorem is given by:

P(A|B) = P(A ∩ B)/P(B)

Here P(A|B) is the probability of condition when event A is occurring while event B has already occurred.

P(A ∩ B) is the probability of event A and event B

The probability of event B is P(B).

Examples and Solutions for Baye's Formula

Some illustrations will improve the understanding of the concept.

Example: Bag I has four white balls and six black balls, whereas Bag II has four white balls and three black balls. One ball is randomly selected from one of the bags and discovered to be black. Determine the likelihood that it came from Bag I.

Sol: Let E1 be the event of choosing bag I, E2 the event of choosing bag II, and the event of a black ball being drawn.

Then,P(E₁) = P(E₂) = 1/2

Also, p(A|E₁) = p

(drawing a black ball from Bag I) = 3/5

(drawing a black ball from Bag II) = 3/7

The possibilities of drawing a black ball from bag I out of two bags can be calculated using Bayes' theorem.

P(E₁|A)=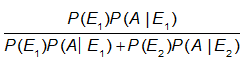

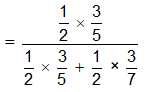
=7/12

To get all the Maths formulas check out the main page. 

Find pdf of Baye's Formula