About Quadratic Function
Quadratic functions are used to acquire values for various parameters in several disciplines of engineering and research. A parabola is used to illustrate them graphically. The curve's direction is determined by the coefficient of the highest degree. The term "quadratic" comes from the word "quad," which meaning "square." Quadratic function is a "polynom of degree 2," in other words. Quadratic functions are employed in a variety of situations.
What do you mean by quadratic Function?
A quadratic function is a polynomial function that has one or more variables and has the largest exponent of two. The polynomial of degree 2 is named after the highest degree term in a quadratic function, which is of the second degree. A second-degree term is the smallest term in a quadratic function. It's an algebraic function.
Quadratic Function Standard Form
A quadratic function has the usual form f(x) = ax2 + bx + c, where a, b, and c are all real values with a≠0.
Examples of Quadratic Function
f(x) = ax2 + bx + c is the quadratic function equation, where a 0. Consider the following instances of quadratic functions:
f(x) = 3x2 + 4x - 5; where a = 3, b = 4, c = -5
f(x) = 4x2 - 9; where a = 4, b = 0, c = -9
f(x) = 3x2 - x; where a = 3, b = -1, c = 0
Now, consider f(x) = 4x-11; where a = 0, thus f(x) is not a quadratic function.
Quadratic Functions Formula
A quadratic function can always be factored, however if the expression's zeroes are non-integer real numbers or non-real values, factorization may be problematic. In such instances, the quadratic formula can be used to find the expression's zeroes. f(x) = ax2 + bx + c is the general form of a quadratic function, where a, b, and c are real numbers with a≠ 0. Roots of quadratic function f(x) may be found by utilising the quadratic function's formula:
x = [ -b ± √(b2 - 4ac) ] / 2a
Different Forms of Quadratic Function
Standard form, vertex form, intercept form are all examples of quadratic functions. The general forms of each of them are as follows:
Standard form of quadratic equation: f(x) = ax2 + bx + c, where a ≠ 0.
Vertex form of quadratic equation: f(x) = a(x - h)2 + k, where a ≠ 0 and (h, k) is The quadratic function is represented by the vertex of the parabola.
Intercept form of quadratic equation: f(x) = a(x - p)(x - q), where a ≠ 0 and (p, 0) and (q, 0) are the parabola's x-intercepts, which represent the quadratic function.
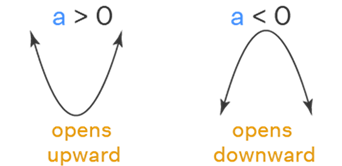
As the value of 'a' changes, the parabola widens upwards or downwards:
- If a > 0, then parabola opens upward.
- If a < 0, then parabola opens downward.
Our experts prepared a List of all Maths formulas used in different calculations.
Find Below Pdf available for downloading for Quadratic Function
