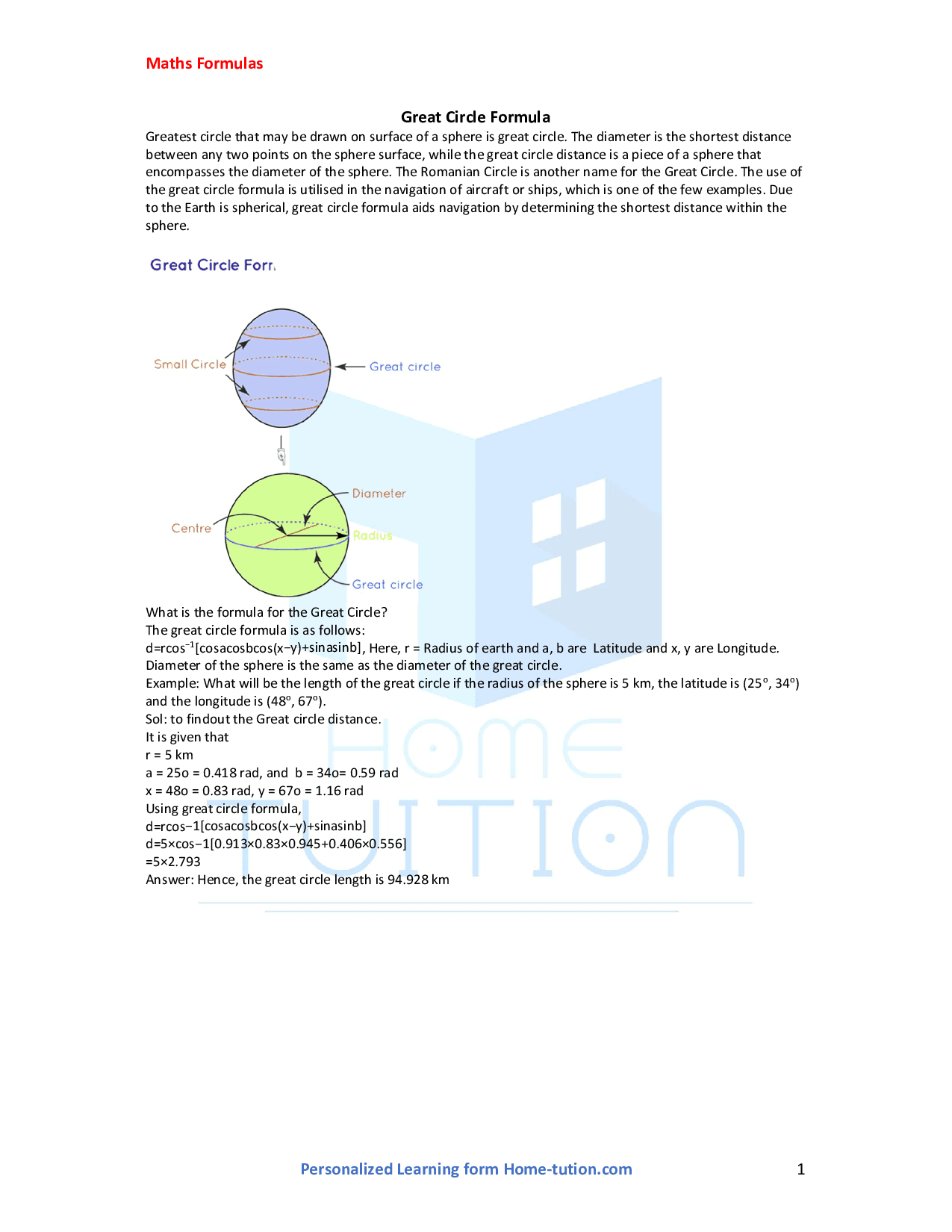
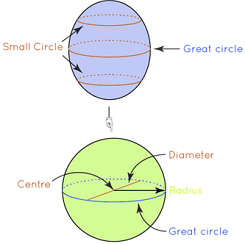
About Great Circle Formula
The greatest circle that may be drawn on the surface of a sphere is a great circle. The diameter is the shortest distance between any two points on the sphere's surface, while the great circle distance is a piece of a sphere that encompasses the diameter of the sphere. The Romanian Circle is another name for the Great Circle. The use of great circle formula is utilised in the navigation of aircraft or ships, which is one of the few examples. Due to the Earth being spherical, the great circle formula aids navigation by determining the shortest distance within the sphere.
What is the formula for the Great Circle?
The great circle formula is as follows:
d = r cos−1[cos a cos b cos(x−y) + sin a sin b],
Here, r = Radius of earth and a, b are Latitude and x, y are Longitude.
The diameter of the sphere is the same as the diameter of the great circle.
Solved example of Great Circle Formula
-
Example: What will be the length of the great circle if the radius of the sphere is 5 km, the latitude is (25°, 34°) and the longitude is (48°, 67°)?
Sol: To find out the Great circle distance.
It is given that r = 5 km
a = 25° = 0.418 rad, and b = 34° = 0.59 rad
x = 48° = 0.83 rad, y = 67° = 1.16 rad
Using the great circle formula,
d = r cos − 1 [cos a cos b cos(x−y) + sin a sin b]
d = 5 × cos − 1[0.913 × 0.83 × 0.945 + 0.406 × 0.556] = 5×2.793
Hence, the great circle length is 94.928 km
Maths Formulas prepared by HT experts are listed on the main page.
Download the pdf of the Great Circle Formula
