About Vector Projection
The projection vector shows how one vector is projected onto another. A scalar value is a vector projection. Cosecant of the angle between the two vectors is multiplied with the provided vector to generate the vector projection of one vector over another.
In physics and engineering, vector projection can be used to represent a force vector about another vector. Get the List of all Maths formulas in one place.
The length of the shadow cast by one vector over another vector is called vector projection. It's calculated by multiplying the magnitude of two vectors by the cosecant of the angle between them. A scalar value is the result of a vector projection formula.
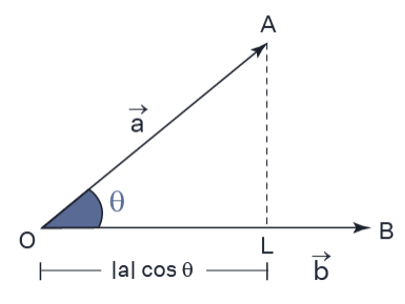
Projection of vector → an over vector →b is obtained by - the product of vector a with the Cosecant of the angle between the vectors a and b. This is further simplified to get the final value of the projection vector. The projection vector has a magnitude which is part of the magnitude of vector a and has the direction same as the vector b.
The product of vector a with the Cosecant of the angle between vectors a and b yields the projection of vector over vector. To acquire the final value of the projection vector, this is simplified even more. The magnitude of the projection vector is equal to that of vector a, and it has the same direction as vector b.
Projection Vector Formula
The dot product of vector a & vector b divided by the magnitude of vector b is the projection vector formula in vector algebra for the projection of vector an on vector b. The dot product's result is a scalar value, & vector b's magnitude is also a scalar value. As a result, the projection vector answer's magnitude and argument are scalar values in the direction of vector b.
Projection of Vector a on Vector b = a.b / |b|