About Polynomial Formula
A polynomial formula is a mathematical expression that expresses a polynomial expression. A polynomial expression is an expression that has two or more terms (algebraic terms). A polynomial expression is created by adding or subtracting binomials or monomials repeatedly. Both like and unlike terms can be found in a polynomial. In polynomials, similar terms are those with the same variable and power, whereas unlike terms are those with distinct variables and powers. Get the List of all Maths formulas in one place.
What is Polynomial Formula?
A polynomial formula is a mathematical statement that represents a polynomial. An expression with two or more terms is called a polynomial expression (algebraic terms). Adding or subtracting binomials or monomials repeatedly produces a polynomial expression. A polynomial can contain both like and unlike terms. Similar phrases in polynomials have the same variable and power, whereas unlike terms have different variables and powers.
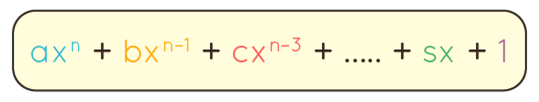
Polynomial Formula
Polynomial Formula is:
(axn+bx{n-1}+cx{n-3}+……+rx+s)(axn+bx{n−1}+cx{n−3}+……+rx+s)
Where
- a, b, c, ..., s are coefficients
- x is the variable
- n is the degree of the polynomial
Some basic formulas associated with the polynomial expression given above are,
where
- F(x) = an(xn)
- a is coefficient
- x is variable
- n is exponent
- F(x) = anxn + an-1xn-1 + an-2xn-2 + ……+ a1x + a0 = 0
- F(x)=an xn +..+ rx + s
- n is natural number
- an−bn=(a−b)(an−1+ an − 2b +…)
- n is a even number
- an + bn = (a + b)(an − 1 − an − 2b +…)
- n is a odd number
- an + bn = (a + b)(an − 1 − an − 2b +…)
Applications of Polynomial Formula
It can be used in engineering, computer science, management, business, and even agriculture. Variables and constants are used to define known and unknown quantities in expressions.
Variables, exponents, and coefficients are used to create polynomial equations. Polynomials can be factored in terms of the degree or variables in the given equation.