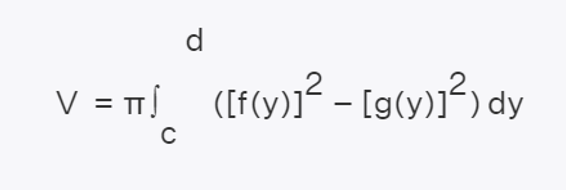About Washer Method Formula
To find volume enclosed between two functions, the washer approach is utilised. We slice the revolution zone perpendicular to the axis of revolution in this manner. Because the slices obtained this way form washers, we name it the Washer Method. To determine the volume of hollow solid of rotation, this method is simply an extension of the disc method.
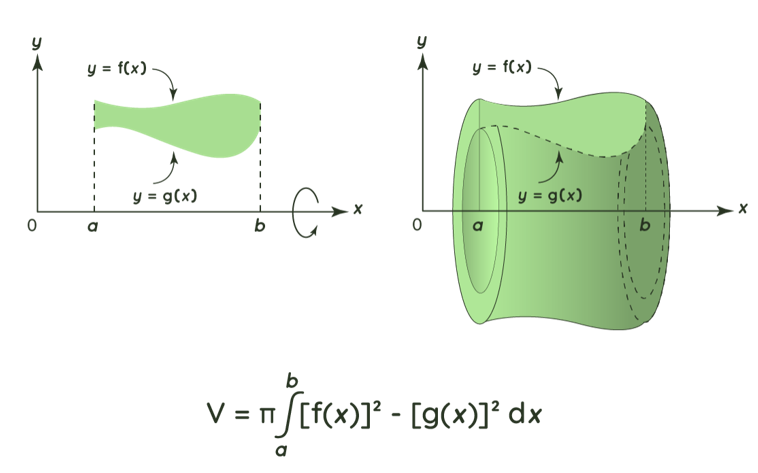
Let y=f(x) and y=g(x) be continuous, non-negative functions in [a,b][a,b] such that g(x)≤f (x). Let R1 be the region in [a,b] that is bordered by two functions f(x) and g(x). The volume of the solid generated by rotating R around the x-axis is equal to
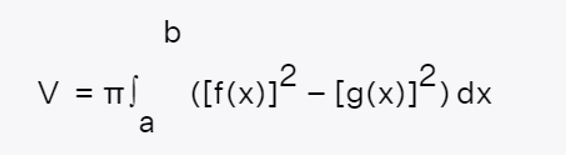
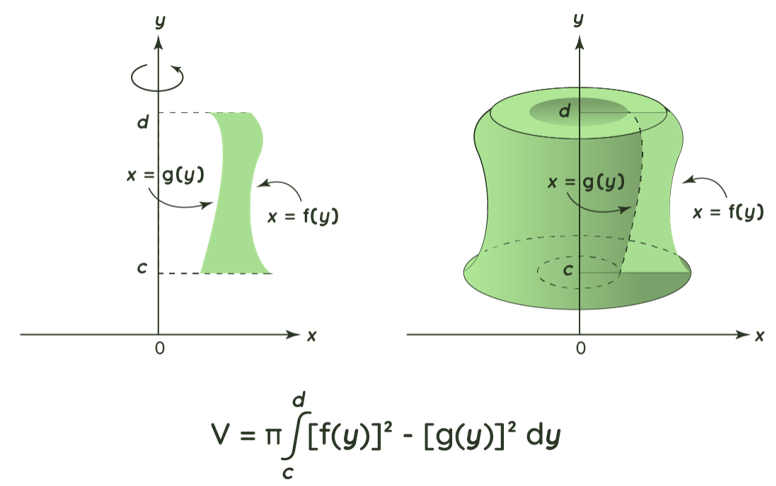
Let R2 be the region bounded by two functions x=f(y) x=g(y) in [c,d] such that g(y)≤f(y). Volume of solid formed by revolving the region R around the y-axis is given by
Find pdf of Washer Method Formula
