Definite Integral Formula

About Definite Integral Formula

The area of a curve in a given graph can be calculated using the Definite Integral. It has boundaries, or start and endpoints, within which the area under a curve is determined. To calculate the area of the curve f(x) with respect to the x-axis, use the limit points [a, b]. The related definite integral expression is ∫abf(x)dx. The total of the areas is integration, and definite integrals are used to calculate the area within limitations. The use of integration to find the area of circles, parabolas, and ellipses dates back to the third century BC. Let's get a better understanding of definite integrals and their properties.

What is a definite integral?

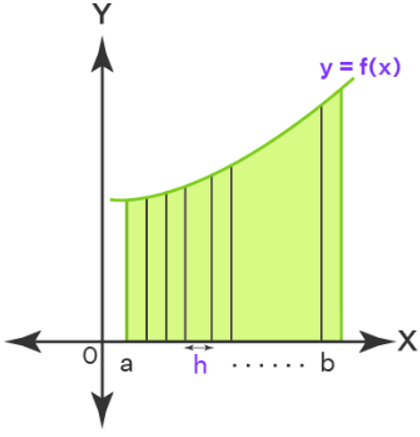
The area under a curve between two set bounds is called a definite integral. For a function f(x) which is defined with reference to the x-axis, the definite integral is expressed as ∫abf(x)dxwhere an is the lower limit and b is the upper limit. We split the area under a curve between two limits into rectangles and add them together to find the area under the curve. The more rectangles there are, the more precise the region is. As a result, we divide the area into an endless number of rectangles, each of the same (very small) size, and then sum all of the areas together. This is the basic notion that underpins definite integrals.

Definite integral formula as the limit sum

The area under a curve can be expressed between two given limits as the sum of an infinite number of rectangles made under the curve. Using this concept, we can evaluate a definite integral ∫axbf(x)dx, area under the curve can be divided into many infinite elementary rectangles by dividing [a, b] into an infinite number of subintervals. Thus, the definite integral as limit sum formula is:

∫abf(x)dx,=limn→∞∑r=1nhf(a+rh)

Here h = (b−a)/n is the length of each subinterval.

Definite integral formula using FTP

A definite integral ∫abf(x)dx can also be evaluated by using the fundamental theorem of calculus (FTC). This formula says first to find out the anti-derivative (indefinite integral) of (x) (and represent it F(x)), substitute the upper limit first and then the lower limit one by one, and subtract the results in order. i.e.,

∫abf(x)dx = F(b) - F(a),Where F'(x) = f(x)

Download pdf of Definite Integral Formula