Chain Rule And Composite Functions

About Chain Rule And Composite Functions

The chain rule is a formula used to compute the derivative of a composite function in differential calculus. If y = f(g(x)), the instantaneous rate of change of function 'f' relative to 'g' and 'g' relative to x results in an instantaneous rate of change of 'f' relative to 'x', according to the chain rule. As a result, the derivative of y will be y' = f'(g(x)). g'(x). One of the most significant laws in distinction is the chain rule.

What do you mean by Chain Rule?

The chain rule is the procedure for determining the derivative of a composite function (e.g., cos 2x, log 2x, etc.). The composite function rule is another name for it. Only composite functions are subject to the chain rule.

Chain Rule Formula

For the function y = f(x), where f(x) is a composite function such that x = g(t), the chain rule formula is:]

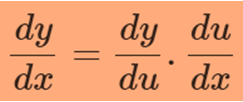
This is the usual form of the differentiation formula chain rule.

Another chain rule formula is as follows:

y' = d/dx (f(g(x) ) ) = f'(g(x)).g'(x)

Chain Rule Composite Function

The following is the definition of a composite function:

(fog)(x) = f(g(x))

Assume that f(x) and g(x) are two differentiable functions, and that the derivative of a composite function f(g(x)) is

(fog)' = (f'o g)× g'

The following example can help you understand this better:

Consider f(x) = e^x2+ 4and g(x) = x²+ 4

Therefore, f'(x) = 2x(e^x2)and g'(x) = 2x

Now, the derivative of a composite function of f(x) and g(x) can be written as:

(fog)' = (f'o g)× g'

To get all the Maths formulas check out the main page. 

Pdf of Chain Rule And Composite Functions