Diagonal of the Square
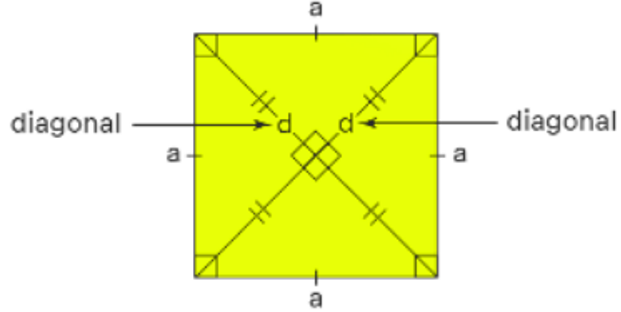
A line segment that connects any two non-adjacent vertices of a square is called it's diagonal. A square has two equal-length diagonals that bisect each other at right angles. When the side length of a square is known, the diagonal of the square formula is used to compute the length of the diagonal. You can get all Maths formulas on one-page visit the Maths Formulas section of HT.
What is the diagonal of the Square?
A square has two diagonals, each of which is produced by linking the square's opposite vertices. For example, examine the following square to see how it relates to the diagonal qualities listed below.
- A square's diagonals are all the same length.
- They are each other's perpendicular bisectors.
- They divide the square into two isosceles right-angled triangles that are congruent.
Diagonal of the square formula
The formula for the diagonal of a square is d = √a. Where 'd' is the diagonal and 'a' is the square's side. The Pythagoras theorem is used to find a square's diagonal formula. A diagonal divides a square into two right-angled isosceles triangles. Both diagonals are congruent and cut each other in half at right angles. Let's look at how to get the formula for finding a square's diagonal.
Derivation of Diagonal of the Square
Consider the triangle ADC formed inside the square as shown in the figure. As all the angles in a square are 90°, using the Pythagoras theorem, we can calculate the value of hypotenuse, which is 'd' in this case.
d2 = a2 + a2
d = √(a2 + a2)
d = √(2a2)
d = √2 × √a2
= √2a
Download the pdf of Diagonal of the Square
