Factorial

About Factorial

Product of whole number 'n' with each & every whole number until 1 is called the factororial. The factorial of 5 is, for example, 5x4x3x2x1, which equals 120. The symbol '!' is used to denote it. So, the value of 5! is 120. A British author named Fabian Stedman defined factorial as the equivalent of change ringing in 1677. The musicians would ring various tuned bells as part of the musical performance known as change ringing. And it was the year 1808 when Christian Kramp, a French mathematician, devised the symbol for factorial: n! The study of factorials is fundamental to many areas of mathematics, including number theory, algebra, geometry, probability, statistics, graph theory, and discrete mathematics, among others.

What Is Factorial?

A number's factorial is the function that multiplies it by each natural number below it. Factorial can be symbolised by the letter "!". The product of the 1st n natural numbers is n factorial, which is written as n!

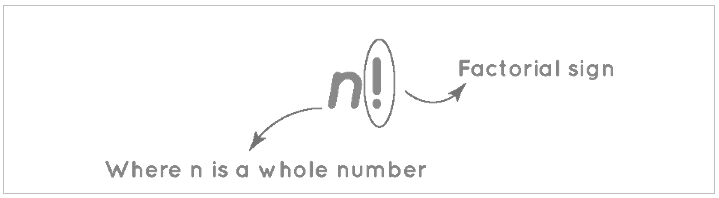
So n! or "n factorial" means: n! = 1. 2. 3…………………………………n =

Product of the first n positive integer = n(n-1)(n-2)…………………….(3)(2)(1)

For example, 5 factorial, that is, 5! can be written as: 5! = 5x4×3×2×1 = 120.

n	n!
1	1	1	1
2	2 x 1	= 2 x 1!	= 2
3	3 x 2 x 1	= 3 x 2!	= 6
4	4 x 3 x 2 x 1	= 4 x 3!	=24
5	5 x 4 x 3 x 2 x 1	= 5 x 4!	= 120

Formula for n Factorial

The formula for n factorial is: n!=n×(n−1)!

n!=n×(n−1)!

What Is 0!

Zero factorial or Factorial of 0 is interesting, and its value is equal to 1, i.e.,0! = 1

Let us see that how this works:

1!=1
2!=2×1=2
3!=3×2×1=3×2!=6
4!=4×3×2×1=4×3!=24
5!=5×4×3×2×1=5×4!=120

Let’s go to the basic formula of factorial n!=n×(n−1)!

How to find 4! What you do is 5!/5. Now, let’s look at the pattern:

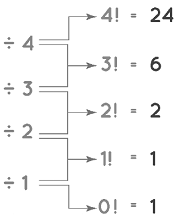
Factorial of Negative Numbers

Can we have factorials for numbers like −1, −2, etc? Let's start with 3!

= 3×2×1 = 6

Let's start with 3!=3×2×1=6 and go down :2!=3!/3=6/3=2

1!=2!/2=2/2=1

0!=1!/1=1/1=1

(−1)!=0!/0=1/0= dividing by zero is undefined

All integer factorials are indeterminate from here on out. As a result, negative integer factorials are unknown.

Use of Factorial

Permutations and combinations are one area where factorials are frequently used. The permutation is an ordered set of outcomes that may be determined using the following formula:

ⁿP_r = n!(n−r)!n!(n−r)!

A combination is a collection of outcomes when the sequence of the outcomes is irrelevant. The formula for calculating it is:

ⁿC_r = n!r!(n−r)!