About P(A ? B) Formula
A set called an intersection B comprises elements that appear in both sets A and B. The intersection of sets A and B is denoted by the symbol ∩, which is written as A∩B and interpreted as 'A intersection B'. The set of elements that are common to all sets is the intersection of two or more sets. The elements that are present in both A and B can simply be used to calculate A∩B.
A∩B is a collection of elements that are found in both A and B. The elements that are present in both A and B are represented by the formula A intersecting B, which is denoted by A∩B. Using the notion of set intersection, the A intersection B formula is as follows: For more Maths formulas click on the main page.
A∩B = {x : x ∈ A and x ∈ B}
B) Formula1.png)
P(A∩B) Formula Definition
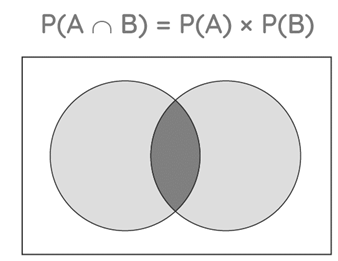
The chance of both independent events "A" and "B" occurring simultaneously is P(A∩B). The sign "∩" denotes an intersection. This formula is used to forecast the outcome rapidly. When two events A and B are independent, we can utilise the multiplication rule, which asserts that the occurrence of one event does not influence the likelihood of the other happening. P(A∩B) = P(A) × P(B). P(A∩B) formula is as follows:
P(A∩B) Formula application
P(A∩B) = P(A) × P(B)
where,
- P(A∩B) = Probability of both independent events “A” and "B" happening together.
- P(A) = Probability of an event “A”
- P(B) = Probability of an event “B”
To calculate P(A∩B) for dependent events, we use the concept of conditional probability and rewrite the formula as,
P(A∩B) = P(A|B)P(B) or P(A∩B) = P(B|A)P(A)
Number of Elements in A∩B
To determine the number of elements in A intersection B, we will use the formula for A union B. We know that the number of elements in A U B is given by n(A U B) = n(A) + n(B) - n(A ∩ B), where
- n(A U B) = Number of elements in the A U B
- n(A) = Number of elements in the A
- n(B) = Number of elements in the B
- n(A ∩ B) = Number of elements in A ∩ B
By taking n(A ∩ B) to one side and all other terms on another side, the formula for the number of elements in A∩B is given as,
n(A) + n(B) - n(A U B) = n(A∩B)
Important Notes on A Intersection B Formula
- {x : x ∈ A & x ∈ B} = A∩B
- A∩B = B∩A
- n(A) + n(B) - n(A U B) = n(A∩B)
- For independent events A and B, P(A) × P(B) = P(A∩B)
- For dependent events A and B, P(A∩B) = P(A|B)P(B) or P(A∩B) = P(B|A)P(A)
Download a free pdf of P(A intersections B)
