Inverse Tangent Formula

About Inverse Tangent Formula

Every function in trigonometry, such as sine, cosine, and tangent, has an inverse function. In a right-angled triangle, the tangent formula is used to calculate the tan of an angle. When we know the side opposite the angle and the adjacent side, we apply the inverse tangent formula to get the angle. arctan or tan^-1 represents the inverse of Tangent.

The trigonometric functions/ratios are:

1. Sine
2. Cosine
3. Tangent
4. Secant
5. Cosecant
6. Cotangent

The inverse of these trigonometric functions are as follows:

1. Inverse Sine
2. Inverse Cosine
3. Inverse Tangent
4. Inverse Secant
5. Inverse Cosecant
6. Inverse Cotangent

The formula for Tan Inverse:

• Tan (A)= Opposite Side / Adjacent Side
• A = Tan^-1(Opposite Side/Adjacent Side)
• Here A is an angle

Solved examples based on Inverse Tangent Formula

Example: If in a triangle, the opposite side to angle A is 1 and the adjacent side is 1/√3

• Sol:
• tan-1 (√3) = A
• As we know, tan 60° = √3
• Therefore, tan^-1(tan 60°) = A
• or A = 60°

Example: Find the value of x from the provided diagram.

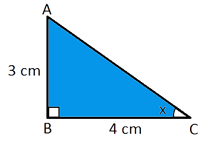
• Sol :
• Since it is given that AB = 3 cm,
• BC = 4 cm
• tan x = AB/BC
• tan x = 3/4 = 0.75
• x = tan^-1(0.75)
• x = 36.9°

Get a List of all Maths Formulas on one page.

Download the pdf of Inverse Tangent Formula