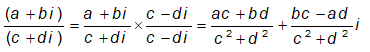Complex Number Formula
About Complex Number Formula
A complex number is one that satisfies the equation i2 = 1 and can be represented in the form a + bi, where a and b are real numbers and i is the imaginary unit. The real part of the complex number is a, while the imaginary part is b in this formula
By employing the horizontal axis for the real part and the vertical axis for the imaginary part, complex numbers extend the concept of the one-dimensional number line to the two-dimensional complex plane.
Here are some Complex Number formulas
- Equality of Complex Numbers Formula
- a + bi = c + di ⇔ a = c and b = d
- Addition of Complex Numbers
- (a + bi) + (c + di) = (a - c) + (b - d)i
- Subtraction of Complex Numbers
- (a + bi) - (c + di) = (a - c) + (b - d)i
- Multiplication of Complex Numbers
- (a + bi) × (c + di) = (ac - bd) + (ad - bc)i
- Multiplication Conjugates
- (a + bi)(a + bi) = a2 + b2
- Division of Complex Numbers
- Powers of Complex Numbers
1. in= i, if n = 4a+1, i.e. one more than the multiple of 4.
Solved example based on Complex Number Formula
Example:
i1 = i; i5 = i;i9 = i; i 4a + 1;
2. in= -1, if n = 4a+2, i.e. two more than the multiple of 4.
Example:
i2 = -1; i6 = -1; i10 = -1;i4a + 2
3. in= -i, if n = 4a+3, i.e. three more than the multiple of 4.
Example:
4. in= 1, if n = 4a, i.e. the multiple of 4. To get all the Maths formulas check out the main page.
Pdf of Complex Number Formula

Related Links
- A plus B Whole Square
- A Plus B Whole Cube Formula
- A Minus B Whole Square
- A minus B Whole Cube Formula
- X plus 1 whole cube Formula
- 2cosA cosB Formula
- 3D Distance Formula
- 30-60-90 Formula
- 90 Degree Angle Formula
- a3 plus b3 Formula
- a3 - b3 Formula
- a2+b2+c2 Formula
- Addition Formula
- All Algebra Formula in One sheet
- Algebraic Sequence Formula
- All Circle Formulas
- Altitude of a Triangle Formula
- Amplitude Formula
- Angle Bisector Theorem
- Angle Difference Formula
- Angles Formulas
- Annuity Formula
- ANOVA Test
- Antiderivative Formula
- APY Formula
- Arccot Formula
- Arc Length
- Arctan Formula
- Area of a circle
- Area of a sector of a circle formula
- Area under the curve formula
- Arithmetic Sequence Recursive Formula
- Arithmetic Mean Formula
- Arithmetic Sequence Explicit Formula
- Arithmetic Sequence Formula
- ASA Formula
- Associative Property Formula
- Asymptote Formula
- A Union B Formula
- Average Deviation Formula
- Average Formula
- Average Rate of Change Formula
- Average speed formula
- Axis of the Symmetry
- Basic Algebra Formula
- Cosec Cot Formula
- Baye's Formula
- Binary to Decimal
- Binomial Distribution Formula
- Binomial Expansion
- Binomial Theorem Formula
- Calculus formulas
- Calculus Formulas
- Celsius Formula
- Celsius to Fahrenheit
- Celsius to kelvin
- Centimeter Square to Meter Square Formula
- Central Angle of a Circle Formula
- Central Limit Theorem
- Central Tendency Formula
- Centroid Formula
- Centroid of a Trapezoid Formula
- Chain Rule And Composite Functions
- Change of Base Formula
- Chi-square formula
- Circle Graph Formula
- Clock Angle Formula
- Coefficient of Variation
- Cofactor Formula
- Coin Toss Probability Formula
- Combinations Formula
- Common Ratio Formula
- Commutative Property Formula
- Completing the Square Formula
- Complex Number Formula
- Conditional probability Formula
- Cone Height Formula
- Confidence Interval Formula
- Consecutive Integers Formula
- Continuous Compounding Formula
- Convert Millimeter to Inches Formula
- Correlation Coefficient Formula
- Cos Inverse Formula
- Cos Square Theta Formula
- Cosecant Formula
- Cost Price Formula
- Cot-Tan Formula
- Cotangent formula
- Covariance Formula
- Cpk Formula
- Cross product formula
- Cube formula
- Cube Root Formula
- Cubic Equation Formula
- Degrees to Radians
- Double Angle Formulas
- Quadratic Function
- Quadrilateral Area Formulas
- Quadrilateral Formulas
- Quarterly Compound Interest Formula
- Quartile Formula
- Quarts to liters formula
- Quotient Rule Formula
- R Squared Formula
- Radians to Degrees
- Radical
- Radius of Curvature Formula
- Radius
- Range Formula
- Rate formula
- Rate of Change Formula
- Rate of Return Formula
- Ratio Analysis Formulas
- Ratio Formula
- Rational Numbers Formula
- Reciprocal Formula
- Recursive Formula
- Reduction Formula
- Regular Hexagon Formula
- Relative Change Formula
- Relative Error Formula
- Relative Frequency Formula
- Relative Standard Deviation Formula
- Remainder Formula
- Lagrange Interpolation Formula
- Lateral Area Formula
- Lateral Surface Area of a Cube
- Law of Cosines
- Law of Sines
- Least Common Multiple
- Limit Formula
- Linear Approximation Formula
- Linear Equation Formula
- Linear Function Formula
- Linear Interpolation Formula
- Litres to gallons formula
- Log Formulas
- Factorial
- Factoring Trinomials Formula
- Factorization Formula
- Fahrenheit Equation
- Fahrenheit to Celsius
- Fahrenheit to Kelvin
- Fibonacci Sequence Formula
- Fibonacci Sequence
- Foil Formula
- Foot To Meter Formula
- Formula For 180 Degree Rotation
- Formula For Absolute Value
- Formula For Adding Fractions
- Formula For Adding Consecutive Numbers
- Formula Arc Length
- Formula For Dividing Fractions
- Formula For Finding Angles
- Formula For Odd Numbers
- Formula For Period
- Formula For Squaring
- Isosceles Triangles Formulas
- Formula To Find x Intercept
- Fourier Series Formula
- Fractions Formula
- Frequency Distribution Formula
- Frequency Formula
- Frustum Of A Regular Pyramid Formula
- Frustum of Cone
- Function Formulas
- Function Notation Formula
- Future Value Compound Interest Formula
- Future Value Simple Interest Formula
- G To Kg Formula
- GCD Formula
- GCF Formula
- Geometric Area Formula
- Geometric Distribution Formula
- Geometric Mean Formula
- Geometric Sequence Formulas
- Geometric Series Formula
- Geometric Sum Formula
- Geometry Formulas
- Gradient Of A Line
- Grams To Kilogram Formula
- Great Circle Formula
- Gross Profit Formula
- Half Life Formula
- Harmonic Mean Formula
- HCF Formula
- Height Of A Parallelogram Formula
- Heron's Formula
- Hexadecimal To Decimal Formula
- Hexagon Formula
- How To Convert 20 Celsius Into Fahrenheit
- How To Convert Celsius Into Fahrenheit
- Hyperbola Formula
- Hyperbolic Functions Formula
- Hypotenuse Formula
- Implicit Differentiation Formula
- Independent Events Formula
- Infinite Geometric Series Formula
- Infinite Series Formula
- Integers Formulas
- Integration By Parts Formula
- Integration Formulas
- Integration of UV Formula
- Interest Formula
- Interest Rate Formula
- Interior Angle Formula
- Internal Rate of Return Formula
- Linear Interpolation Formula
- Interquartile Range(IQR) Formula
- Inverse Functions
- Inverse of Matrix
- Inverse Tangent Formula
- Inverse Trigonometric Formulas
- Inverse Variation Formula
- Inversely Proportional Formula
- Perimeter Of The Isosceles Triangle
- Sample Mean Formula
- Sample Size Formula
- Sample Standard Deviation Formula
- Sample Variance
- SAS Triangle Formula
- Scalene Triangle
- Scientific Notation Formula
- Secant Formula
- Selling Price Formula
- Long Division Formula
- Sequences and Series Formulas
- Semicircle Formulas
- Sequence Formulas
- Maclaurin Series Formula
- Magnitude of a Vector
- Sets Formulas
- Magnitude of Vector formula
- P(A/B) Formula
- Matrix Formula
- Mean Absolute Deviation Formula
- Parabola Formula
- Mean Deviation
- Parallel Lines Formula
- Parallelogram Formula
- Mean formula
- Pearson Correlation Formula
- Percent Composition Formula
- Mean Median Mode Formula
- Mean Value Theorem
- Median
- Midpoint Formula
- Miles to Km formula
- Percent Decrease Formula
- Measurement Formulas
- Miles to meter formula
- Percent Error
- Percent Difference Formula
- Percent Yield
- ml to l Formula
- Percentage Increase Formula
- Mode
- Monthly Compound Interest Formula
- Mph to m/s formula
- Percentile Formulas
- Multiple Angle Formulas
- Multiplication
- n Choose k Formula
- Perfect Cube Formula
- Natural Log Formula
- Perfect Square Formula
- NCR Formula
- Perfect Square Trinomial Formula
- Net Change Formula
- Net Income Formula
- Net Present Value Formula
- Perimeter Formulas
- Net Worth Formula
- Newton's Method Formula
- Nominal Interest Rate Formula
- Normal Distribution Formula
- nPr Formula
- Ordinary Annuity Formula
- Orthocenter Formula
- Perimeter Of A Circle Formula
- Z Score
- Perimeter Of A Kite Formula
- Perimeter of a Trapezoid Formula
- Yards to Meters Formula
- Permutation And Combination
- Y-Intercept
- Permutation Formula
- Work Formula
- What are Trigonometric Functions Formulas
- Weight formula
- Perpendicular Line Formula
- Phase Shift Formula
- Weighted Mean
- Weighted Average
- Pi Formula
- Point of Intersection Formula
- Washer Method Formula
- Point Slope Form
- Volume Formulas
- Vieta's Formula
- Venn Diagram Formula
- Vector Projection
- Vector formulas
- Poisson Distribution Formula
- Polygon Formula
- Polynomial Formula
- Variance Formula
- U Substitution Formula
- Unit Vector
- Population Change Formula
- Unit Rate Formula
- Unit Conversion
- Unit Circle
- Uniform Distribution Formula
- Population Mean Formula
- Trigonometry Formulas
- Triangular Pyramid Formula
- Triangle Formulas
- Trapezoidal Rule
- Trajectory Formula
- Total Interest Formula
- Time Formula
- The direction of a vector
- The Accuracy Formula and How to Calculate It
- Temperature Conversion
- T Distribution Formula
- Taylor Series Formula
- Taylor Polynomial Formula
- Tangent Line
- Tangent Formulas
- Tangent Circle Formula
- Tan Formula
- Tan2x Formula
- Surface-area-of-triangular-pyramid-formula
- Surface Area of a Square Prism
- Surface Area Formulas
- Supplementary Angles Formula
- Sum of Squares
- Sum of Perfect Squares Formula
- Sum of n Natural Numbers Formula
- Sum of Integers Formula
- Sum of Exterior Angles Formula
- Sum of Even Numbers Formula
- Sum of Cubes Formula
- Sum of Arithmetic Sequence Formula
- Sum of Angles Formula
- Summation Formulas
- Subtraction
- Stirling Formula
- Standard Form Formula
- Standard Deviation
- SSS Formula
- Square Root
- Square Footage Formula
- Speed formula
- Special Right Triangles
- Special Factoring Formulas
- Slope of the Secant Line Formula
- Slope Intercept Form
- Slope Formula
- Slant Height Formula
- Skewness Formula
- Sin Squared x Formula
- Sin Formula
- Sine Formula
- Sin Cos Tan
- Sin Cos Formulas
- Sin2x Formula
- Simpson's Rule
- Simple Interest
- Similar Triangles Formula
- Signal to Noise Ratio
- Sides of Triangle
- Shell Method Formula
- Rotation Formula
- Root Mean Square Formula
- Rise Over Run Formula
- Right Angled Triangle
- Riemann Sum Formula
- Rhombus Formula
- Reverse Percentages
- Revenue Formula
- Resultant Vector Formula
- Remainder Theorem
- Profit Margin Formula
- Profit Formula
- Profit and loss formula
- Product To Sum Formulas
- Area of Square Formula
- Product Rule
- Area of Trapezoid
- Basic Statistics Formula
- Current Formula
- Daily Compound Interest Formula
- De Moivre's Formula
- Exponential Decay Formula
- Decimal to Binary Formula
- Decimals Formula
- Definite Integral Formula
- Derivative Formula
- Diagonal of a Cube Formula
- Diagonal of a Parallelogram
- Diagonal of a Polygon Formula
- Diagonal of The Rectangle
- Probability Formula
- Prime Numbers Formula
- Diagonal of the Square
- Diagonals Formula
- Prime Factorization Formula
- Present Value Formula
- Present Discounted Value Formula
- Population Variance
- Diameter Formula
- Km to miles formula
- Diameter Of A Sphere Formula Using Volume
- Kilogram to newton formula
- Exterior Angle Theorem
- Difference of Cubes Formula
- Exponential Formula
- Difference of Squares Formula
- Exponential Growth Formula
- Exponential growth and decay formula
- Exponential Function formula
- Exponential Function
- Side Angle Side Formula
- Difference Quotient Formula
- Differential Equation Formula
- Dimensional Formula
- Discriminant Formulas
- Disk Method Formula
- Distance Formula
- Distributive Property Formula
- Exponential Equations
- Dividend Divisor Quotient Remainder Formula
- Exponential Distribution
- Exponential Decay Formula
- Division Formula
- Euler's Formula
- Expected Value Formula
- Dot product
- Euclidean Distance Formula
- Double Angle Formulas
- Equilateral Triangle Formula
- Equation of a circle formula
- Endpoint Formula
- Double Time Formula
- Empirical Rule Formula
- Empirical Probability Formula
- Ellipse Formulas
- Effective Interest Rate Formula
- Effective Annual Rate Formula
- Differentiation and Integration Formula
- Direct Proportion Formula
- Direct Variation Formula
- a2-b2 Formula
- Discount Formula
- Determinant Formula
- Pythagorean Triples Formula
- P-value Formula
- Proportion Formula
- P(A intersections B) Formula
- P(A union B)Formula
- Decimal to Hexadecimal
- Vertex Formula
- Area of Octagon
- Outlier Formula
- Distance Between Two Points Formula