Binary to Decimal

About Binary to Decimal formulas

The binary to decimal conversion process involves converting a number in the binary number system to its decimal equivalent. A number system is a set of rules for representing numbers. The binary number system is used to represent data in computers and electronic systems, and it only has two digits: 0 and 1. The decimal number system is the most widely used and most easily comprehended number system in the world. It is made up of digits ranging from 0 to 9. Starting with the right-most digit, which has a weight of 1, you can convert binary to decimal by adding the products of each binary digit with its weight (which is of the form - binary digit 2 increased to power of the position of the digit) starting from right-most digit. which has a weight of 2⁰.

The positional notation approach and the doubling method are two methods for converting binary to decimal. Let's look at the various binary to decimal conversion methods.

Related links: Great Circle Formula | Gross Profit Formula | Half Life Formula
Also Check: Harmonic Mean Formula | HCF Formula

What is Binary to Decimal Conversion?

The binary to decimal conversion is used to represent a number in the Binary Number System to its decimal equivalent. To represent numbers, a number system is necessary. Every number system has a base, which is determined by the total number of digits in the system. The binary number system, for example, has a base of two since any number is represented by only two digits. Similarly, the decimal number has a base of ten since each number is represented by ten digits.
The binary to decimal conversion is significant because it allows you to read numbers that are represented as series of 0s and 1s.

Binary to Decimal Conversion Methods

The binary to decimal conversion is done to make it easier to interpret huge binary values in a human-readable format. There are two ways to convert a binary number to a decimal value.

• Positional Notation
• Doubling

Binary to Decimal Conversion by Positional Notation Method

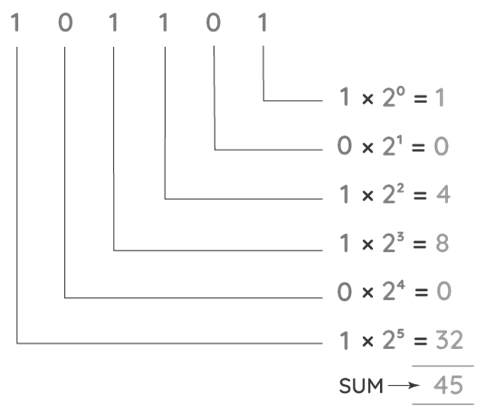
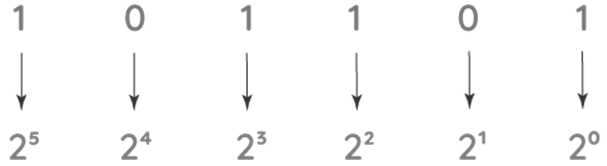
Step 1:Starting with the rightmost digit, write down the powers of 2 for each of the digits. The first power would be 2^0, followed by 2^1, 2^2, 2^3, 2^4, 2^5, and so on. Because there are 6 digits in the provided example, the weight of each place from the right is 2^0,2^1,2^2,2^3,2^4,2^5, starting with the rightmost digit.

•  

Step 2:Now, starting from the right, multiply each digit in the binary number by its associated weight based on its position, and assess the result. To understand the step, look at the diagram below. Finally, add up all of the products obtained for each of the binary digits.

• 

   

Step 3: Assign a decimal value to the binary number.

• :(101101)2(101101)2=(45)10(45)10

Binary to Decimal Conversion Using Doubling Method

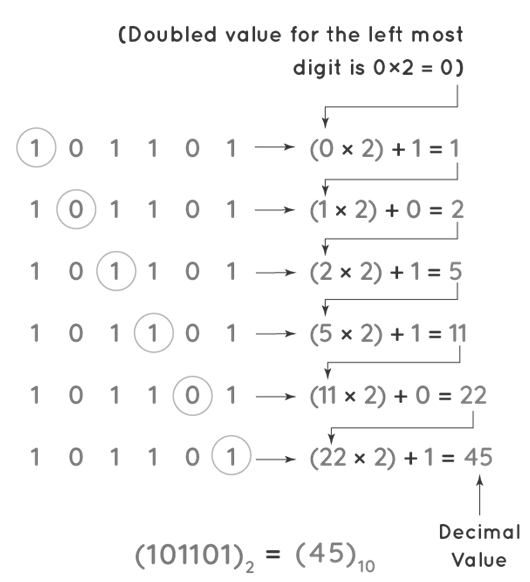
Step 1:Begin writing the binary number with the left-most digit. Add the current digit to the previous number and double it. We consider the double of the previous digit as 0 because we are starting from the left-most digit and there is no previous digit to the left-most digit. The left-most digit in (101101)2(101101)2 is '1', for example. The previous number's double is 0. As a result, we obtain ((0 x2) + 1), which is 1.

Step 2:Repeat the technique for the next digit as well. The second from the left digit is 0. Now multiply the previous digit by two and add it to the current one. As a result, we obtain [(1 2) + 0], which is 2.

Step 3:Continue in this manner for all of the digits. The true decimal value is the sum obtained in the last step. As a consequence of applying the doubling method to convert the binary number (101101)2(101101)2 to a decimal, the output is 45104510.

Observe the figure given below to relate to the steps and understand how the doubling method works.

 

Binary to Decimal Conversion Formula:

(Decimal Number)₁₀=(d0× 2⁰)+(d1× 2¹)+(d2× 2²)+ ..... +(dn−1× 2^n-1)

where,d0d0,d1d1,d2d2are the individual digits of the binary number starting from the right-most position.

Let us see the application of the above binary to decimal formula and learn how to convert binary to a decimal using the following example.

Binary to Decimal Conversion Chart

The binary to the decimal conversion of the first 20 decimal numbers is displayed in the chart given below.

 

Binary	Decimal
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10
1011	11
1100	12
1101	13
1110	14
1111	15
10000	16
10001	17
10010	18
10011	19
10100	20

To get all the Maths formulas check out the main page. 

Find pdf of solved example and use of Binary to Decimal formulas