About Remainder Theorem
When a polynomial is divided by a linear polynomial, the remainder theorem is used to get the remaining. The remaining is the number of items left over after a particular number of items are sorted into groups with an equal number of items in each group. After division, it is something that "remains." Let's have a look at the remainder theorem.
What Is the Remainder Theorem?
The remaining theorem goes like this: The remainder is obtained by r = a when a polynomial a(x) is divided by a linear polynomial b(x) whose zero is x = k. (k). The remainder theorem allows us to calculate the remainder of any polynomial divided by a linear polynomial without actually performing the division algorithm steps.
Remainder Theorem Formula
p(x) = (x-c)q(x) + r is the generic formula for the remainder theorem (x). To show the remainder theorem formula, we'll use polynomials.
When p(x) is divided by (x-a)
Remainder = p(a)
OR
When p(x) is divided by (ax+b)
Remainder = 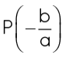
Proof for the Remainder Theorem
Dividend = (Divisor × Quotient) + Remainder.
r(x) is constant then, p(x) = (x-c)·q(x) + r.
Let’s put x=c
p(c) = (c-c)·q(c) + r
p(c) = (0)·q(c) + r
p(c) = r
Hence, proved.
Important Notes about Remainder Theorem
The remainder is obtained by r = a when a polynomial a(x) is divided by a linear polynomial b(x) whose zero is x = k. (k)
- p(x) = (x-c)q(x) + r(x). is the remainder theorem formula
- Dividend = (Divisor × Quotient) + Remainder.

