About Cosecant Formula
The cosecant ratio, often known as cosec or csc, is one of the six trigonometric ratios. In a right triangle, the cosecant formula is the hypotenuse's length divided by the opposite side's length.
What is Cosecant Formula?
For a given right triangle ABC, where A is an acute angle, as shown below:
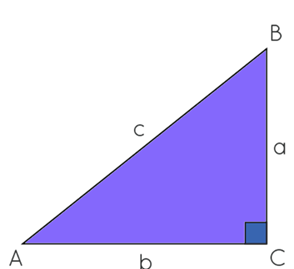
AB = Hypotenuse
AC = Between angle A and right angle is a side adjacent to angle A.
BC = Side opposite to angle A
The following is the cosecant formula:
cosec A = hypotenuse / opposite side = AB / BC = c / a
We know that,
sin A = opposite side / hypotenuse
The reciprocal of sine is cosecant. As a result, cosec A in terms of sin A is equal to
cosec A = 1 / sin A = 1 / (a / c) = c / a
Hence, we can say that the trigonometric ratios cosec and sin has a reciprocal relationship among them.
Cosine Rule
The Cosine Rule states that the square of the length of any side of a triangle is equal to the sum of the squares of the other sides minus twice the product of the other two sides multiplied by the cosine of angle included between them in trigonometry. The law of cosines is also known as the Cosine Formula.
Suppose, a, b and c are lengths of the side of a triangle ABC, then;
|
a2= b2+ c2– 2bc cos ∠x b2= a2+ c2– 2ac cos ∠y c2= a2+ b2– 2ab cos ∠z |
where∠x,∠y and∠z are the angles between the sides of the triangle.
The cosine rule applies to the lengths of a triangle's sides when one of its angles is a cosine angle. We can use this rule to determine the length of a triangle's side or the angle between the sides.

What are the Laws of Cosine?
As per the diagram, Cosine rules to find the length of the sides a, b & c of the triangle ABC is given by;
a2= b2+ c2– 2bc cosx
b2= a2+ c2– 2ac cos y
c2= a2+ b2– 2ab cos z
Similarly, to find the angles x, y and z, these formulae can be re-written as :
cos x = (b2+ c2-a2)/2bc
cos y =(a2+ c2-b2)/2ac
cos z =(a2+ b2– c2)/2ab
Our experts prepared a List of all Maths formulas used in different calculations.

