About Fractions Formula
The fractions formula makes it easier to conduct a variety of fraction operations. The basic arithmetic operations for fractions differ from those for normal integral values. Fraction formulas make it simple to do fundamental fraction operations. The denominators of the fractions must be identical for the basic arithmetic operation of addition or subtraction. By calculating the reciprocal of the second fraction, the division of one fraction by another fraction is changed into multiplication. In this lesson, we'll study more about the fraction formula and solve a few cases.
What is Fractions Formula?
One of the most significant components of arithmetic that we use in our daily lives is fractions. Fractions are numerical values that are a portion of a larger number and are represented by the symbol / (also known as the fractional line), for example, a/b. The formulae for fractions aid in the formulation of rules to be followed when doing the four basic arithmetic operations of addition, subtraction, multiplication, and division. The fractions formulas are listed below:
Formula 1
A mixed fraction has both a full number and a fraction. The numerator of the improper fraction is formed by multiplying the denominator with the whole number and adding it to the numerator of the mixed fraction.
- A b/c = [Ac + b]/c
Formula 2
The simple addition of numerators and the use of the same denominator for the answer allows for the addition of like fractions. The final answer's denominator is the same as the denominator of the given fractions.
- a/b + c/b = [a + b/c]
Formula 3
Each of the fractions is multiplied with appropriate constants to make the denominators of the two fractions equal for the addition of unlike fractions. Before starting the addition operation, the goal is to make the denominators of the fractions equal.
- [a/b + c/d = a.d/b.d + c.b/d.b = ad + bc/bd]
Formula 4
Fractions can be multiplied by multiplying the numerators and then the denominators of both fractions, and then expressing the result as a single fraction. To achieve the final solution, this product is further simplified and decreased.
- a/b x c/d = ac/bd
Formula 5
By first inverting the fraction in the denominator and then multiplying it with the numerator fraction, division of fractions becomes multiplication of fractions.
- a/b/c/d = a/b x d/c
- Adding fraction with whole numbers
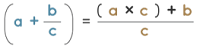
- Adding fraction with like denominators
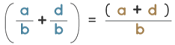
- Adding fraction with different denominators
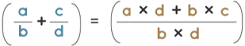
- Multiplication of Fraction
a/b x c/d = ac/bd - Division of Fractions
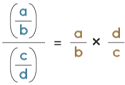
- Where,
a, b, c and d are constants
Fraction Formulas
The following are the other significant formulas we use: To see if two fractions are comparable, use the cross multiply rule:
When a/b = c/d, ad = bc To reverse the numerator and denominator, use the reciprocal rule: if a/b is the fraction, then b/a is reciprocal.
Get the list of all Maths formulas used in general calculations.