About Fibonacci Sequence
Leonardo Pisano Bogollo, an Italian, was the first to discover the Fibonacci sequence (Fibonacci). The Fibonacci sequence is made up of entire numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. The Fibonacci sequence is the name given to an endless sequence. Starting with 0 and 1, each phrase is the sum of the two preceding ones. This is known as "nature's secret code." Sunflowers, daisies, broccoli, cauliflowers, and seashells all have spiral designs that follow the Fibonacci sequence. Let's find out more about it and its intriguing characteristics.
What is Fibonacci Sequence?
In simple terms, the Fibonacci sequence states that every number in the sequence is the sum of two numbers before it in the sequence. The following are the first 20 Fibonacci numbers:
| F0 = 0 | F10 = 55 |
| F1 = 1 | F11 = 89 |
| F2 = 1 | F 12 = 144 |
| F 3 = 2 | F 13 = 233 |
| F 4 = 3 | F 14 = 377 |
| F 5 = 5 | F 15 = 610 |
| F 6 = 8 | F 16 = 987 |
| F 7 = 13 | F 17 = 1597 |
| F 8 = 21 | F 18 = 2584 |
| F 9 = 34 | F 19 = 4181 |
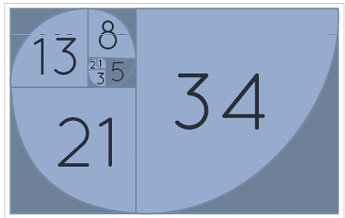
Fibonacci Spiral
The spiral displayed here represents the Fibonacci sequence. The spiral illustrates the Fibonacci number pattern. This spiral begins with a rectangle with the golden ratio (1.618) as its length and width. There are two squares in this rectangle. The squares are then further divided. The spiral is drawn inside these squares, connecting the corners of the boxes. The Fibonacci sequence becomes closer to the golden ratio as the numbers get larger.
Fibonacci Sequence Formula
Setting F0 = 0, F1 = 1, and using the formula below to determine Fn, the Fibonacci sequence formula for "Fn" is defined using the recursive formula. The Fibonacci formula can be found here.
Fn= Fn-1+ Fn-2, where n > 1
| n | Term | F(n - 1) | F(n - 2) | Fn = F(n - 1) + F(n - 2),(for n > 1) |
| 0 | First | - | - | F0 = 0 |
| 1 | Second | F0 = 0 | - | F1 = 1 |
| 2 | Third | F1 = 1 | F0 = 0 | F2 = 0 + 1 = 1 |
| 3 | Fourth | F2 = 1 | F1 = 1 | F3 = 1 + 1 = 2 |
| 4 | Fifth | F3 = 2 | F2 = 1 | F4 = 2 + 1 = 3 |
| 5 | Sixth | F4 = 3 | F3 = 2 | F4 = 3 + 2 = 5 |
| 6 | Seventh | F5 = 5 | F4 = 3 | F6 = 5 + 3 = 8 |
Note that F0 is termed as the 1st term here (but NOT F1). The Fibonacci sequence has the following intriguing properties:
| A | B | A/B |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6 |
| 5 | 8 | 1.6 |
| 8 | 1 | 1.625 |
| 144 | 233 | 1.618055555555556 |
| 233 | 377 | 1.618025751072961 |
- The golden ratio is connected to Fibonacci numbers. The golden ratio can be used to calculate any Fibonacci number, Fn =(Φn - (1-Φ)n)/√5, φ is golden ratio and Φ ≈ 1.618034. find 7th term, we apply F7 = [(1.618034)7 - (1-1.618034)7] / √5 = 13
- The "golden ratio" is the ratio of successive Fibonacci numbers. Let A and B be the Fibonacci sequence's two consecutive numbers. B/A thus approaches the Golden Ratio. We may use the formula above to discover any term in the Fibonacci sequence.
- The approximated Fibonacci number is obtained by multiplying the preceding Fibonacci number by the golden ratio (1.618034). 13 is a number in the sequence, for example, and 13 × 1.618034... = 21.034442. The next Fibonacci number after 13 in the sequence is 21.
- A multiple of n is every nth number. Examine the series for another pattern of interest. Every third number in the sequence is a two-digit multiple. Every fourth number is a multiple of three, and every fifth number is a multiple of five.
- The Fibonacci sequence can also be used below zero. F-n = (-1)n+1 Fn is the formula. For instance, F-4 = (-1)5. F4 = (-1)3 = -3.
- The sum of n terms of Fibonacci Sequence is given by Σi = 0n Fi = Fn+2 - F2 (or) Fn+2 - 1, where Fn is the nth Fibonacci number. (Note: the first term starts from F0)
Applications of Fibonacci Sequence
The Fibonacci sequence can be found in many different places, including nature, music, and the human body. Employed in coding (computer algorithms, interconnecting parallel, and distributed systems) in a variety of domains of science, including high-energy physics, quantum mechanics, and cryptography, among others.