Trapezoidal Rule

About Trapezoidal Rule

The trapezoidal rule can also be said as the trapezoid rule or trapezium rule. It is a technique for approximating definite integral in numerical analysis. The trapezoidal rule is an integration rule used to find the area under a curve by dividing the curve into small trapezoids. The addition of all areas of small trapezoids will give the area under the curve. Now take a look at the trapezoidal rule formula. Get the List of all Maths formulas in one place.

What is the Trapezoidal Rule?

Trapezoidal rule is applied to solve definite integral of the form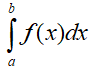, by approximating the region under the graph of function f(x) as a trapezoid and evaluating its area. Under the trapezoidal rule, we can solve the area under a curve which is by dividing the total area into little trapezoids rather than rectangles.

Trapezoidal Rule Formula

We apply the trapezoidal rule formula to solve a definite integral by calculating the area under a curve by dividing the total area into little trapezoids rather than rectangles. This rule is used for approximating definite integrals where it uses the linear approximations of the functions. The trapezoidal rule takes the average of the left and the right sum.

Assume y = f(x) be continuous on [a, b]. Here,we divide interval [a, b] into n equal sub-intervals and hence, each of width will be h = (b - a)/n,

such that a = x₀< x₁ < x₂ < ? < x_n = b

Area = (h/2) [y₀ + 2 (y₁ + y₂ + y₂ + ..... + y_(n-1)) + y_n]

here,

y₀, y₁,y₂…. are values of function at x = 1, 2, 3….. respectively.

Download free pdf of Trapezoidal Rule Its Use And Solved Examples