About Sum of n Natural Numbers Formula
The arithmetic progression (A.P) formula, where the common difference between the preceding and subsequent numbers is 1, yields the sum of the natural numbers formula. Natural numbers, often known as counting numbers, range from 1 to infinity, for example, 1,2,3,4,5,6,7, and so on. Check out the List of Maths Formulas.
To find 1 + 2 + 3 +.... up to n terms, use the sum of n natural numbers formula. This is organised in arithmetic order. As a result, the formula for the sum of natural numbers is derived using the formula for the sum of n terms in the arithmetic progression.
Sum of Natural Numbers Formula: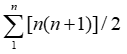
where n is a natural number.
Definition of Sum of n Natural Numbers (N)
The sum of n natural numbers is an arithmetic progression in which the sum of n terms is organised in a series with the first term being 1, n being the number of terms, and the nth term being the nth term. [n(n+1)]/2 represents the sum of n natural numbers. Natural numbers are those which begin with one & conclude with infinity. Except for the number 0, natural numbers contain only whole numbers.
Derivation of Sum of Natural Numbers Formula
- In an AP, let's calculate the sum of natural numbers using the sum of n terms. 'a' is the first term in an AP, 'd' is a common difference, and 'l' is the nth term, l = a+(n-1)d.
- The common difference between the integers in the arithmetic series of natural numbers is 1.
- Sum of n terms of arithmetic progression (A.P) will be:
- Sum = a + (a+d) + (a+2d) ………… + (l-2d) + (l-d) + l———– (1)
- The order is reversed, the sum remains the same, so,
- Sum = l+(l-d)+(l-2d)+(I-2d)…………+(a+2d)+(a+d)+a———- (2)
- Adding eq (1) & (2):-
- (a+l)+[(a+d)+(l-d)]………….+[(l-d)+(a+d)]+(l+a)] =2 × Sum
- (a+l)+(a+l)…+(a+l) = 2× Sum
- 2 × Sum = n×(a+l)
- ⇒ n/2(a+l) = Sum
- Putting the value of l from the previous equation :-
- Sum of n terms of arithmetic progression = n/2[2a + (n – 1)d]
- For natural numbers, a = 1 & d = 1, therefore,
- n/2[2×1+(n-1)1] = S
- [n(n+1)]/2 = S
- Hence, the sum of natural numbers formula = [n(n+1)]/2
Download free pdf of Sum of Perfect Squares Formula Its Use And Solved Examples
