About Stirling Formula
The Stirling formula, often known as the Stirling approximation, is used to calculate the approximate factorial value of a given integer (n! or Γ(n) for n >>). James Stirling was the inspiration for the name. The Stirling formula is an excellent approximation formula since it makes it easy to compute the factorial of bigger numbers and gives exact results for small values of any number, such as 'n'. The Stirling formula is also utilised in practical mathematics for the Gamma function.
What do you mean by Stirling Formula?
The Stirling formula yields a factorial value for a number that is very near to the real value of the factorial of the number, with an error of less than 2%. The Stirling approximation was named after James Stirling and is used to estimate the approximate value of factorial of a given number 'n'. The Stirling formula is as follows:
n! =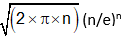
Example: Find value of 5 factorial using Stirling formula.
Sol: To Find factorial of 5, we have
Using Stirling Formula
n! =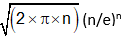
5! =
= 118.019
To get the list of Maths formulas check out the main page.
Download a free pdf of Stirling Formula Its Use And Solved Examples
