About Euclidean Distance Formula
Let us first define Euclidean distance before learning the Euclidean distance formula. Euclidean distance is the distance between two points in coordinate geometry. The length of a segment connecting the two places is measured to find the two points on a plane. The Pythagoras theorem is used to derive the Euclidean distance formula.
As its name implies, the Euclidean distance formula calculates the distance between two points (or the straight line distance). Let's pretend that (x1,y1) and (x2,y2) are two points on a two-dimensional plane. The Euclidean distance formula is shown below.
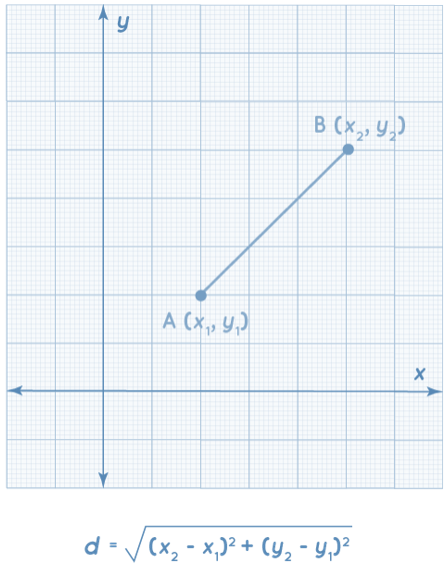
What is Euclidean Distance Formula
d = √[ (x2 – x1)2 + (y2 – y1)2]
where,
- (x1, y1) - coordinates of one point.
- (x2, y2) - coordinates of the other point.
- d - the distance between (x1, y1) and (x2, y2).
Euclidean Distance Formula Derivation
Consider two places A (x1, y1) and B (x2, y2) and suppose that d is the distance between them to construct the Euclidean distance formula. A line segment connects A and B. To find the formula, make a right-angled triangle with the hypotenuse AB. As seen below, we construct horizontal and vertical lines from A and B that intersect at C.
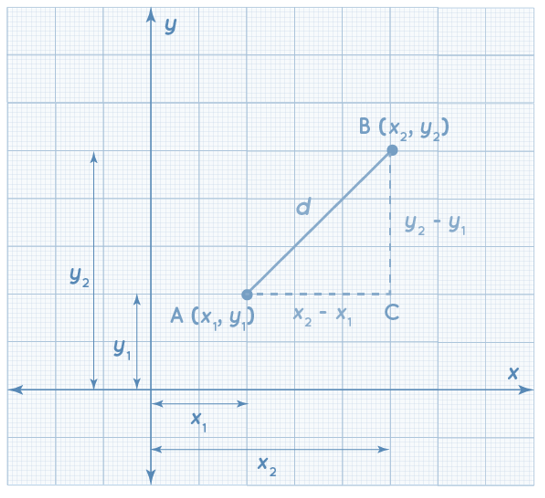
Apply the Pythagoras theorem to triangle ABC.
AB2 = AC2 + BC2
d = (x2 – x1)2 + (y2 – y1)2
Taking the square root on both sides,
d = √[ (x2 – x1)2 + (y2 – y1)2]
The euclidean distance formula is derived.
Download free pdf Euclidean Distance Formula
